Matematik

Differentialligninger

09. august 2019 af marielinge - Niveau: A-niveau

Kan nogen hjælpe?

Vedhæftet fil: Skærmbillede 2019-08-07 kl. 11.57.01.png

Brugbart svar (0)

Svar #1
09. august 2019 af ringstedLC

a) Når y(t) er vandmængde som funktion af tiden må stigningen være den afledte y '(t) af mængden. Vandmængden til tiden 0 er opgivet.

$\begin{align*} y'(0) &= 360000-0.004\cdot 10^7\;,\;y(0)=10^7 \end{align*}$

$\begin{align*} \text{Differentialligningen}:\\y' &= b-a\cdot y \\ \text{har l\o sningen}:\\ y &= \tfrac{b}{a}+c\cdot e^{-ax}\;,\;c=\text{ integrationskonstanten} \\\\ y'(t) &= 360000-0.004\cdot y(t) \\ y(t) &= \;? \\ y(0) &= 10^7\Rightarrow c=\;? \text{ (husk at}\;e^{-a\,\cdot \,0}=e^0=1) \\ y(48) &= \;? \end{align*}$

Svar #2
10. august 2019 af marielinge

a) jeg løser differentialligningen og får y(t) efter. hvad gør jeg med y(t) efter?

Brugbart svar (0)

Svar #3
10. august 2019 af ringstedLC

#2: Det er ikke nødvendigt at løse den, da y(0) er opgivet og kan indsættes som i #1.

Svar #4
10. august 2019 af marielinge

er lidt forvirret. det er jo en hastighed jeg skal ende ud med som svar?

Brugbart svar (0)

Svar #5
10. august 2019 af MatHFlærer

Ved $t=0$ er $y(0)=10^7$ ifølge oplysningen, altså at der er $10^7$ kubikmeter vand til tidspunktet $t=0$ .

Din differentialligning er $y'(t)=360000-0.004\cdot y(t)$ . Du ønsker at finde ud af hastigheden ved $t=0$ . Du ved så heldigvis også, hvor meget vandmængden er, ved netop $t=0$ som så er ${\color{Red} 10^7}$ kubikmeter, så hastigheden kan du beregne ved

$y'(t)=360000-0.004\cdot {\color{Red} 10^7}=...$ Hastigheden er $m^3/t$

Så som skrevet i #3 er det ikke nødvendigt at løse differentialligningen til spgm. a).

Læs #1. Anvender du CAS, som Maple? Der kan du anvende kommandoen:

${\color{Red} \texttt{\textbf{dsolve(\{y'(t)=360000-0.004*y(t),y(0)=10\^\;7\},y(t))}}}$

Brugbart svar (0)

Svar #6
10. august 2019 af ringstedLC

#4: OK, - du får oplyst, at y(0) = 10⁷ og at funktionen y(t) er vandmængden til tiden t. Stigningen (hældningen) af denne funktion må derfor være y '(t). Og da:

$\begin{align*} y'(t) &= 360000-0.004\cdot y(t)\Downarrow \\ y'(0) &= 360000-0.004\cdot y(0)\Downarrow \\ y'(0) &= 360000-0.004\cdot 10^{7}\Downarrow\;,\;y(0)=10^{7} \\ y'(0) &= \;? \end{align*}$

I a) skal du altså "bare" indsætte et "x" i en afledt funktion på formen:

$\begin{align*} f'(x) &= 360000-0.004x\;,\;x=10^7 \\ f'(10^7) &= \;? \end{align*}$

fordi der er givet et talpar (0, 10⁷). På nedenstående figur har jeg selvfølgelig måttet beregne vandmængdefunktionen for at tegne den, men du kan jo godt beregne hældningen af en tangent i et punkt når den afledte er opgivet, uden at kende selve funktionen.

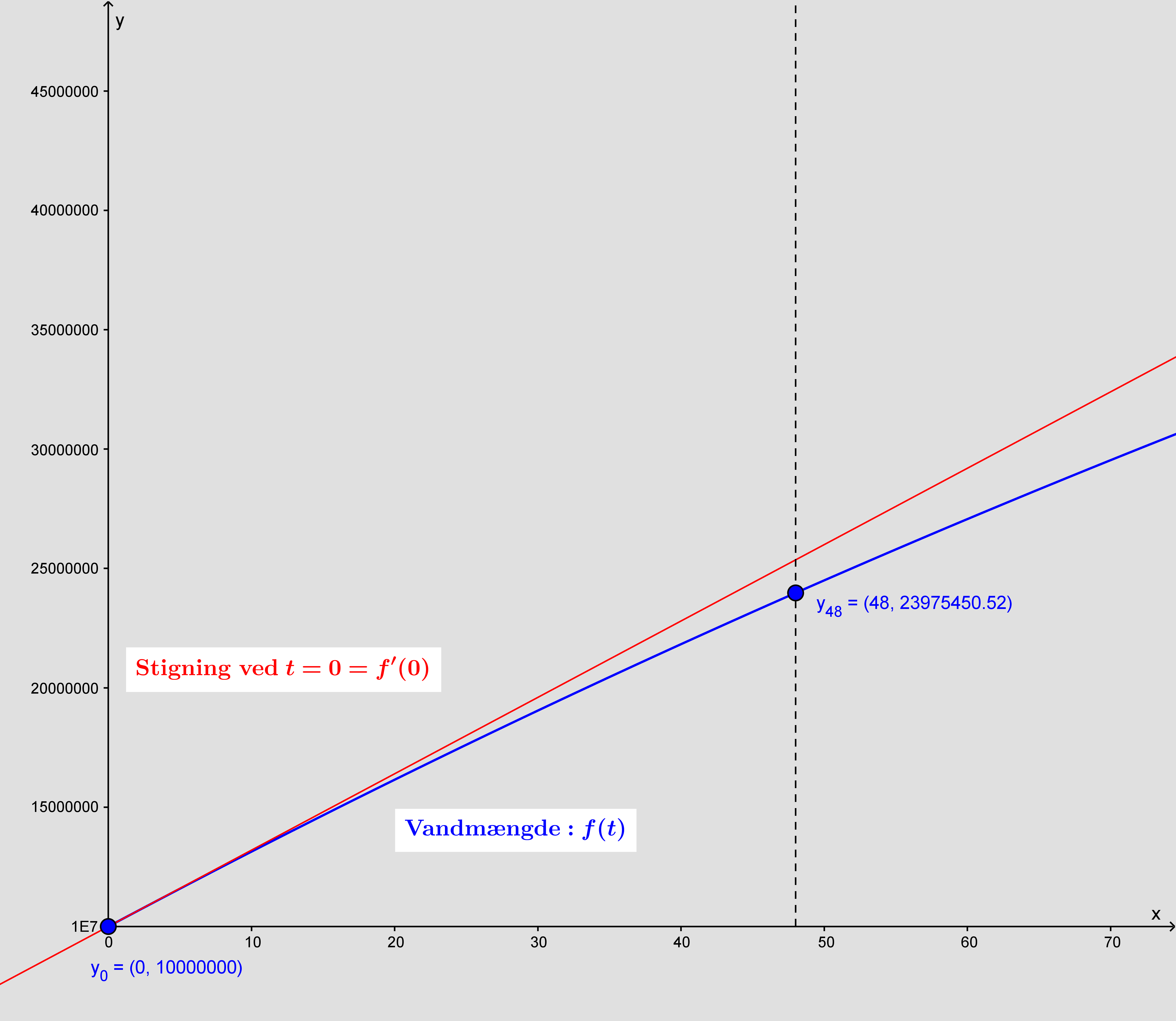
Det er en typisk diff.-ligning opgave. Et a), hvor man pr. automatik tænker, at man må løse ligningen, når nu der er en ligning, men blot behøver at indsætte et opgivet talpar.

I b) er det så nødvendigt at beregne y(t) som i #1

Brugbart svar (0)

Svar #7
10. august 2019 af ringstedLC

Vedhæftet fil:A_M_073 - Vandres., Diff.lign._marielinge.png

Skriv et svar til: Differentialligninger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.