Matematik

Stamfunktion

15. september 2019 af Mie23234 - Niveau: A-niveau

HJÆÆÆÆLP!

Vedhæftet fil: Skærmbillede 2019-09-15 kl. 14.28.07.png

Brugbart svar (1)

Svar #1
15. september 2019 af StoreNord

a)
Du skal finde en stamfunktion til f.
En stamfunktion til 1/x er ln(|x|)

Brugbart svar (1)

Svar #2
15. september 2019 af Bibo53

Der gælder, at $g$ er en stamfunktion til $f$ , hvis og kun hvis $g'=f$ . Du skal derfor undersøge, om $g'=f$ og $g(1)=9$ . Ingen af delene gælder. For eksempel er

$g'(x)=\frac{1}{2}\cdot 2(x+1)+\frac{1}{x}+4x+3=5x+4+\frac{1}{x}$

(Det er også et problem, at $g$ kun er defineret for $x>0$ .)

Brugbart svar (1)

Svar #3
15. september 2019 af StoreNord

Det er der nu delte meninger om: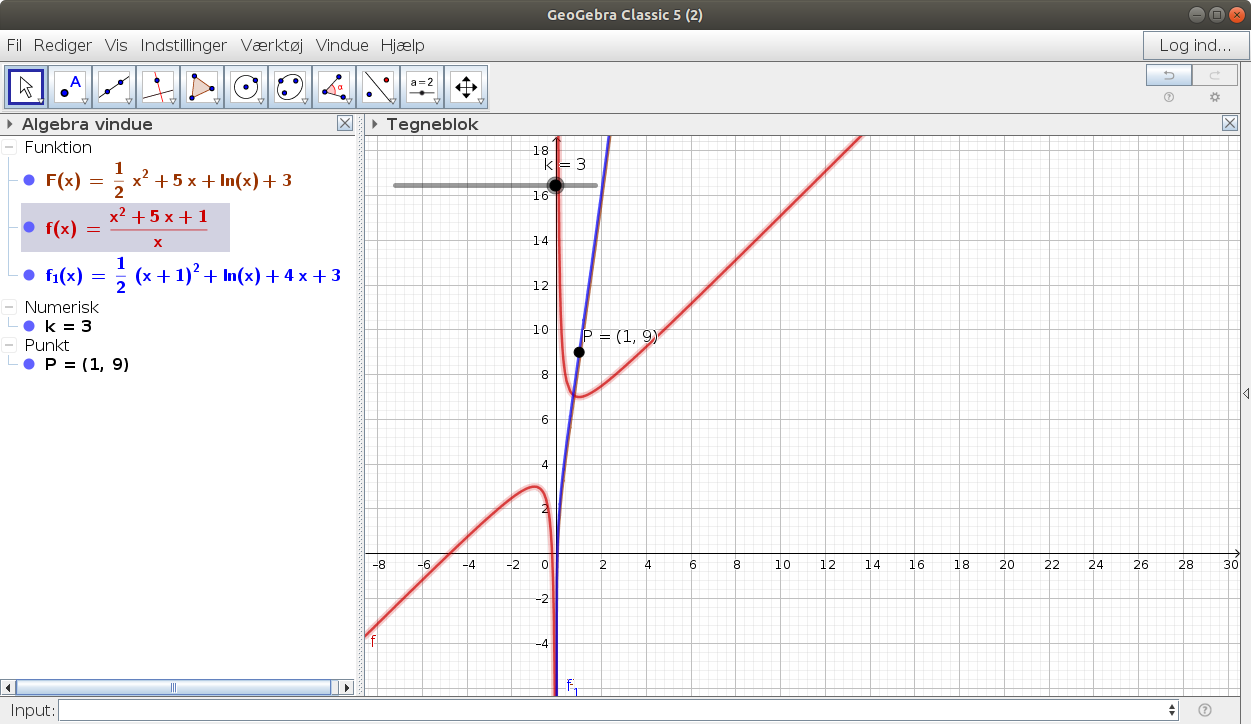 Skærmbillede fra 2019-09-15 14-55-43.png

Vedhæftet fil:Skærmbillede fra 2019-09-15 14-55-43.png

Brugbart svar (0)

Svar #4
15. september 2019 af ringstedLC

Brugbart svar (1)

Svar #5
15. september 2019 af Bibo53

Undskyld, det er korrekt at $g(1)=9$ , men $g$ er ikke er en stamfunktion til $f$ .

Brugbart svar (0)

Svar #6
15. september 2019 af StoreNord

Det siger Geogebra ellers.

Brugbart svar (0)

Svar #7
15. september 2019 af Bibo53

Er det ikke korrekt, at $g'(x)=5x+4+\frac{1}{x}\ne f(x)$ ?

Brugbart svar (0)

Svar #8
15. september 2019 af mathon

Brugbart svar (0)

Svar #9
15. september 2019 af mathon

$\small \small \small \small \small \small\begin{array}{llll}& g{\, }'(x)=\frac{1}{2}\cdot 2\cdot (x+1)+\frac{1}{x}+4\\\\ &g{\, }'(x)=x+1+\frac{1}{x}+4\\\\ &g{\, }'(x)=x+\frac{1}{x}+5=f(x)\\ \textup{og}\\ &g(1)=\frac{1}{2}\left ( 1+1 \right )^2+\ln(1)+4\cdot 1+3=9\\\\ \textup{hvorfor}&g(x)\textup{ er den stamfunktion til f, som g\aa r gennem (1,9).} \end{array}$

Brugbart svar (0)

Svar #10
15. september 2019 af StoreNord

#7
Det er slet ikke relevant at tale om g'.

Brugbart svar (0)

Svar #11
15. september 2019 af Bibo53

#10 Jo, det er det nu. Men jeg kan se, at jeg har regnet forkert. Den korrekte udregning er

$g'(x)=\frac{1}{2}\cdot 2(x+1)+\frac{1}{x}+4=x+5+\frac{1}{x}$

Svaret på spørgsmålet er derfor ja, under forudsætning af, at vi ændrer definitionen af $f$ til

$f(x)=x+5+\frac{1}{x},\;\;x>0$ .

Brugbart svar (0)

Svar #12
15. september 2019 af mathon

dog har #9 kun gyldighed, såfremt Dm(f) = R₊, hvilket ikke er tilfældet.

Brugbart svar (0)

Svar #13
15. september 2019 af AMelev

#7 Nej, det er ikke korrekt (jf #9eller tjek med CAS) - jeg tror, du har glemt at differentiere 4x - men metoden i #2 er fin, og her er g' selvfølgelig relevant.

Metoden i #3 er en anden metode, som dog involverer brug af hjælpemidler

En tredje (mere besværlig) metode er at bestemme stamfunktion F til f og fastlægge konstanten, så grafen for g₁(x) = F(x) + k går gennem punktet P(1,9)
$?F(x)=\int (x+5+1/x)dx=$ $?$ F(x) = ∫f(x) dx = ∫(x+5+1/x)dx = ½x² + 5x + ln(x) for x > 0
g₁(1) = 9 ⇔ F(1) + k = 9 ⇔ 11/2 + k = 9 ⇔ k = 7/2, dvs. g₁(x) = ½x² + 5x + ln(x) + 7/2
g(x) = ½(x + 1)² + 4x + ln(x) + 3 = ½x² + x + ½ + 4x + ln(x) + 3 = ½x² + 5x + ln(x) + 7/2 = g(x)

Skriv et svar til: Stamfunktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.