Matematik
Forklaring af omskrivning af en ligning
Hej, jeg har en opgave jeg sidder lidt fast på. Jeg har en ligning, hvor den så er blevet omskrevet på en anden måde gennem nogle regler og jeg skal skrive min tankegang ned om hvad der foregør. Problemet er at jeg ikke kan finde ud af hvilke regler der er blevet brugt, eller hvorfor ligningen kan se sådan ud efter forandringen. Jeg har lagt før og efter ligningen ind som vedhæftet fil.
Svar #1
22. november 2019 af SuneChr
Reducér hvert led først. Der er ingen grund til, at der står 4·2 i første led og 2/2 i sidste led.
Ordn leddene så det ligner en pæn 2.grads ligning. Først alt med x2 og så x. Vi slipper her
for konstantleddet. Der er benyttet fælles faktor, der er sat udenfor parentes.
I anden linje ville det have set pænere ud, om h var kommet hen foran parentesen (8 + ),
men gør ellers ingen forskel.
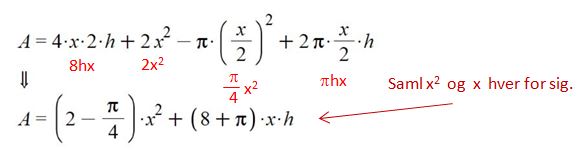
Svar #2
23. november 2019 af MathiasMan
Spændende, jeg sidder med samme opgave, men hvor kommer 8 fra i (8 + pi)? Og er "pi * (x/2)^2" rykket helt forrest i ligningen? Og nu er der lige pludselig ingen minus tegn uden for paranteserne mere ?? Jeg er meget forvirret over disse opgaver :/
Svar #3
23. november 2019 af iliojacobsen
Svar #4
23. november 2019 af iliojacobsen
Svar #5
23. november 2019 af iliojacobsen
Skriv et svar til: Forklaring af omskrivning af en ligning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






