Matematik

Differentialligninger

21. januar 2020 af Larsdk4 (Slettet) - Niveau: A-niveau

Er denne opgave korrekt udregnet

Vedhæftet fil: Udklip.PNG

Brugbart svar (0)

Svar #1
21. januar 2020 af mathon

Svar #2
21. januar 2020 af Larsdk4 (Slettet)

Eller på denne måde

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #3
21. januar 2020 af mathon

$\small \begin{array}{lllll} &y{\, }'=-y+3x^2-10\\\\&y{\, }'+y=3x^2-10&\textup{panserformlen benyttes}\\\\&y=e^{-x}\cdot \int e^x \left ( 3x^2-10 \right )\mathrm{d}x&\textup{partiel integration benyttes flere gange}\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -\int e^x\cdot 6x\; \mathrm{d}x\right )\\\\&y=e^{-x}\cdot \left ( e^x\cdot (3x^2-10) -6\int e^x\cdot x\; \mathrm{d}x \right )\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -6\cdot \left ( e^x\cdot x -\int e^x\cdot 1\; \mathrm{d}x\right ) \right )\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -6\cdot e^x\cdot x+6\cdot e^x+C \right )\\\\&y=3x^2-10-6x+C\cdot e^{-x}\\\\\\&y=C\cdot e^{-x}+3x^2-6x-10 \end{array}$

Svar #4
21. januar 2020 af Larsdk4 (Slettet)

#3
$\small \begin{array}{lllll} &y{\, }'=-y+3x^2-10\\\\&y{\, }'+y=3x^2-10&\textup{panserformlen benyttes}\\\\&y=e^{-x}\cdot \int e^x \left ( 3x^2-10 \right )\mathrm{d}x&\textup{partiel integration benyttes flere gange}\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -\int e^x\cdot 6x\; \mathrm{d}x\right )\\\\&y=e^{-x}\cdot \left ( e^x\cdot (3x^2-10) -6\int e^x\cdot x\; \mathrm{d}x \right )\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -6\cdot \left ( e^x\cdot x -\int e^x\cdot 1\; \mathrm{d}x\right ) \right )\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -6\cdot e^x\cdot x+6\cdot e^x+C \right )\\\\&y=3x^2-10-6x+C\cdot e^{-x}\\\\\\&y=C\cdot e^{-x}+3x^2-6x-10 \end{array}$

Tak men kan du give mig et tips begynde denne opgave

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #5
21. januar 2020 af mathon

tastekorrektion:

$\small \small \begin{array}{lllll} &y{\, }'=-y+3x^2-10\\\\&y{\, }'+y=3x^2-10&\textup{panserformlen benyttes}\\\\&y=e^{-x}\cdot \int e^x \left ( 3x^2-10 \right )\mathrm{d}x&\textup{partiel integration benyttes flere gange}\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -\int e^x\cdot 6x\; \mathrm{d}x\right )\\\\&y=e^{-x}\cdot \left ( e^x\cdot (3x^2-10) -6\int e^x\cdot x\; \mathrm{d}x \right )\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -6\cdot \left ( e^x\cdot x -\int e^x\cdot 1\; \mathrm{d}x\right ) \right )\\\\&y=e^{-x}\cdot\left ( e^x\cdot (3x^2-10) -6\cdot e^x\cdot x+6\cdot e^x+C \right )\\\\&y=3x^2-10-6x+6+C\cdot e^{-x}\\\\\\&y=C\cdot e^{-x}+3x^2-6x-4 \end{array}$

Brugbart svar (0)

Svar #6
21. januar 2020 af mathon

for $\small C=0$ er

$\small y=3x^2-6x-4\quad \textup{en partiel l\o sning.}$

Svar #7
21. januar 2020 af Larsdk4 (Slettet)

#6
for $\small C=0$ er

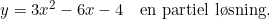
$\small y=3x^2-6x-4\quad \textup{en partiel l\o sning.}$

Kunne du give mig et tips i forhold til den anden opgave ?

Brugbart svar (0)

Svar #8
21. januar 2020 af mathon

Brugbart svar (0)

Svar #9
21. januar 2020 af mathon

$\small \small \begin{array}{lllll} &f(x)=y=\int x\cdot \cos(2x)\, \mathrm{d}x\\\\&y=x\cdot \frac{1}{2}\cdot \sin(2x)-\frac{1}{2}\int \sin(2x)\cdot 1\, \mathrm{d}x\\\\&y=f(x)=\frac{1}{2}\cdot x\cdot \sin(2x)+\frac{1}{4}\cos(2x)+k\\\textup{samt}\\&f\left ( \frac{\pi }{2} \right )=\frac{1}{2}\cdot f(\pi )\\\\\\&\frac{1}{2}\cdot \frac{\pi }{2}\cdot \sin(2\cdot \frac{\pi }{2})+\frac{1}{4}\cos(2\cdot \frac{\pi }{2})+k=\frac{1}{2}\cdot \left ( \frac{1}{2}\cdot \pi \cdot \sin(2\cdot \pi)+\frac{1}{4}\cos(2\cdot \pi)+k \right )\\\\&0+\frac{1}{4}\cdot (-1)+k=\frac{1}{2}\cdot \left ( 0+\frac{1}{4}\cdot 1+k \right )\\\\&-\frac{1}{4}+k=\frac{1}{8}+\frac{1}{2}k\\\\&\frac{1}{2}k=\frac{1}{8}+\frac{1}{4}\\\\&k=\frac{2}{8}+\frac{2}{4}\\\\&k=\frac{1}{4}+\frac{2}{4}\\\\&k=\frac{3}{4}\\\\\\&f(x)=\frac{1}{2}\cdot x\cdot \sin(2x)+\frac{1}{4}\cdot \cos(2x)+\frac{3}{4} \end{array}$

Brugbart svar (0)

Svar #10
21. januar 2020 af AMelev

# 7 Husk lige én tråd pr. opgave, ellers bliver det et rodsammenn.

Mht. den oprindelige opgave er din anden metode også brugbar og nok egentlig lettere/sikrere.
Tjek i øvrigt dine løsninger med dit CAS-værktøj, så kan du måske selv finde ud af, hvor fejlen i 1. metode ligger.

En lidt anden måde at skrive det op på, men i princippet det samme:
y = a·x² + b·x + c
y' = -y + 3 x² - 10 ⇔ 2a·x + b = -(a·x² + b·x + c) + 3 x² - 10 ⇔ 2a·x + b = (3 - a) x² - b·x - c -10
Da polynomierne skal være ens for alle x, skal koefficienterne i de enkelte stemme overens parvis, så
3 - a = 0 ⇔ a = 3, 2a = -b ⇔ b = -2a = -6 og b = -c - 10 ⇔ c = -b - 10 = -4
y = 3·x² - 6·x - 4

Brugbart svar (0)

Svar #11
21. januar 2020 af AMelev

Ad #7 & #9 Partiel integration indgår ikke i kernestoffet på STX, og det er den bekendtgørelse Gymnasial supplering følger, ikke?.
Hvorfor bruger du ikke dit CAS-værktøj? Til eksamen har du næppe tid til at lave disse opgaver i hånden.

Skriv et svar til: Differentialligninger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.