Matematik

Integral

28. januar 2020 af DeepOcean - Niveau: B-niveau

hej : jeg har brug for lidt hjælp vedr følgende opgave:

En vask skal have et profil som vist i figuren. Kurven følger funktionsforskriften f(x) = −5 · 10−5 x4 + 0,06 x2.

1_Hvor meget vand kan der være i vasken?

svar:jeg mener at volumen kam man få her ved at rotere funktion på x.aksen med med intervalerne[0,25]

er det rigtigt ?

2_Vasken støbes ned i betoncylinder med de angivne mål. Hvor meget beton skal bruges til støbningen?

jeg mener at den skal roteres på y-aksen med intervaller [-30,30] ?

er det rigtig?

Vedhæftet fil: csm_144_Vask_omdrejningslegeme_c71e8dec04.png

Brugbart svar (0)

Svar #1
28. januar 2020 af AMelev

Hvorfor er denne opgave B-niveau og den anden, du har lagt op A-niveau?

Læg lige et billede af hele opgaven op - jeg kan ikke tyde forskriften.

Svar #2
28. januar 2020 af DeepOcean

$f(x) = -5*10^-5 *x^4 +0,06x^2$

her får du funktion overskrift.

Den opgave er A niveau og ikke B ( indtesting fejl)

Brugbart svar (1)

Svar #3
28. januar 2020 af ringstedLC

$\begin{align*} A_{\,vask,\,tv.-snit}(x) &= A_{rektangel,\;1}(x)-A_{f(x)}(x) \\ &= x_1\cdot f(x_1)-\int_{0}^{x_1}f(x)\,dx\;,\;x_1>0\;,\;f(x_1)=f_{maks.} \\ V &= 2\pi\cdot \int_{0}^{x_1}x\cdot A_{\,vask,\,tv.-snit}(x)\,dx \end{align*}$

2. Bemærk f(0) = 0.

$\begin{align*} A_{\,beton,\,tv.-snit}(x) &= A_{rektangel,\,2}(x)-A_{f(x)}(x) \\ &= 30\cdot \left(30-f(30)\right)+\int_{0}^{30}f(x)\,dx \\ V &= 2\pi\cdot \int_{0}^{30}x\cdot A_{\,beton,\,tv.-snit}(x)\,dx \end{align*}$

Svar #4
28. januar 2020 af DeepOcean

Hvor meget værdien af x1 i først del af opgave .?

Brugbart svar (0)

Svar #5
28. januar 2020 af ringstedLC

x₁: Se betingelsen i 2. linje

Svar #6
29. januar 2020 af DeepOcean

kan vi sige at rektangel areal er 60 * 30 ?

Svar #7
29. januar 2020 af DeepOcean

i Først del ,kan man finde tvasnit areal med følgende måde :

$(30*30) )- \oint_{0}^{30} f(x) dx$ ?

i Anden del :

hvorfor ? $+ \oint_{0}^{30} f(x) dx$ . Er er ikke nok med tvsnit areal er : 30 * 30 - 30* f(30)

Brugbart svar (0)

Svar #8
29. januar 2020 af AMelev

#2 Bem. Hvis der er mere end ét tegn ved opløftet/sænket, skal { } omkring f(x) = -5*10^{-5} *x^4 +0,06x^2

#3 Jeg forstår ikke beregningerne. A'erne er jo uafhængige af x. Og hvor kommer den anvendte formel for V fra?

Brugbart svar (1)

Svar #9
30. januar 2020 af ringstedLC

#6: Nej. De 30 cm er højden på betonen og har intet at gøre med volumet af vasken. Vasken og rektangel, 1 har højden f_maks som bestemmes ved at differentiere f , x > 0. Løsningen til f '(x) = 0 benævnes x₁. Denne indsættes i de to arealfunktioner og arealet af den punktmængde, der skal drejes, kan bestemmes.

#8: A'erne er funktioner af x. V er volumet af omdrejningslegemet omkring y-aksen.

Vedhæftet fil:__0.png

Brugbart svar (1)

Svar #10
30. januar 2020 af ringstedLC

#3, 2. rettelse:

$\begin{align*} A_{beton,\,tv.-snit}(x) &= A_{rektangel,\,2}(x)\,{\color{Red} +}\,A_{f(x)}(x) \end{align*}$

Vedhæftet fil:__1.png

Brugbart svar (1)

Svar #11
30. januar 2020 af ringstedLC

#9 og #10: Beklager mgl. indsættelse af figurer, - min browser er vist blevet træt.

Brugbart svar (0)

Svar #12
30. januar 2020 af AMelev

#3
1.

$A_{\,vask,\,tv.-snit}(x) &= A_{rektangel,\;1}(x)-A_{f(x)}(x) \\ &= x_1\cdot f(x_1)-\int_{0}^{x_1}f(x)\,dx\;,\;x_1>0$

Når du beregner det, giver det jo et tal, ikke en funktion af x, da såvel x1 som 0 er konstanter.
Tilsvarende i 2.

Jeg er med på, at det er volumen af omdrejningslegemet om y-aksen, der skal bestemmes, men hvordan kommer du frem til formlerne i #3?
Jeg ville mene, den skulle hedde $V=\pi\cdot \int_{0}^{y1} x^2 dy$ , hvor y1 = f(x1) og y = f(x) skal omskrives til
x = f^-1(y), som skal indsættes.

Svar #13
30. januar 2020 af DeepOcean

Hej ringstedLC :

1000 tak for din hjælp , nu har jeg løst opgave :)

Brugbart svar (0)

Svar #14
30. januar 2020 af ringstedLC

#13: Selv tak. Desværre må jeg meddele at 2. ikke er rigtig. Vender tilbage i weekenden, håber du kan vente.

Brugbart svar (1)

Svar #15
02. februar 2020 af ringstedLC

#3: Rettelse. Man må ikke lave én funktion af arealerne, når volumet bestemmes som et omdrejningslegeme.

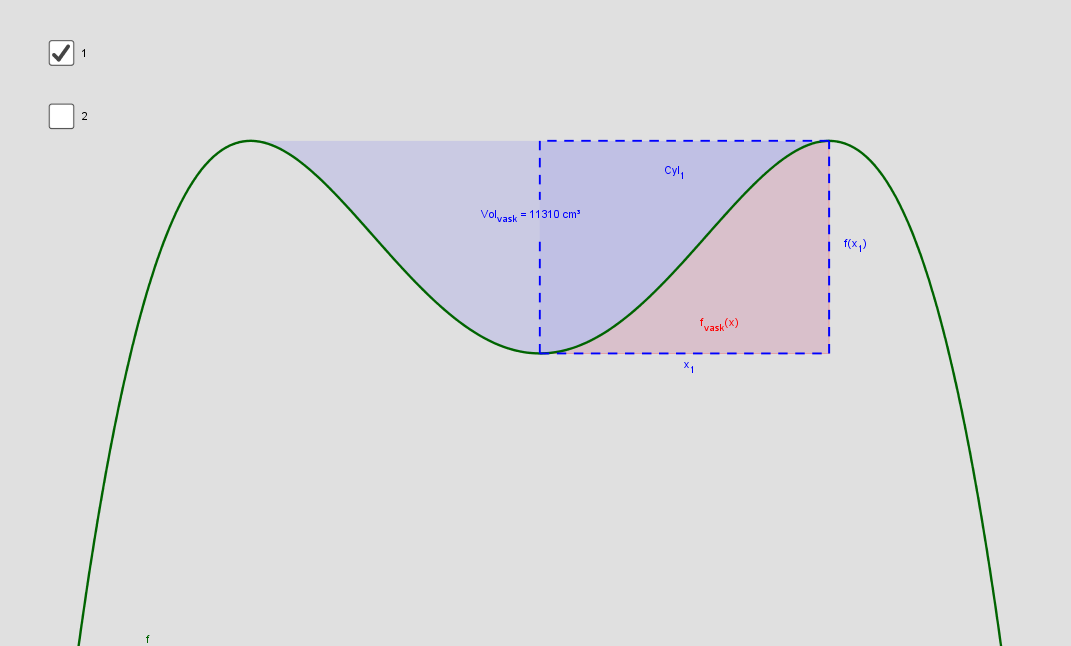
1. Indholdet af vasken: En cylinder minus rumfanget af noget af det grå:

$\begin{align*} f'(x) &= 0\;,\;x>0\Rightarrow x=x_1=10\sqrt{6}\Rightarrow f(x_1)=18 \\ Cyl_{1}(x) &=f(x_1)\;,\;0\leq x\leq x_1 \\ Vol_{vask} &= 2\pi\cdot \left (\int_{0}^{x_1}x\cdot Cyl_{1}(x)\,dx- \int_{0}^{x_1}x\cdot f(x)\,dx \right ) \\ &= 2\pi\cdot 1800\approx 11310\,(cm^3) \end{align*}$

Vedhæftet fil:A_M_086_1 - Vask, omdr.- legeme_DeepOcean.png

Brugbart svar (1)

Svar #16
02. februar 2020 af ringstedLC

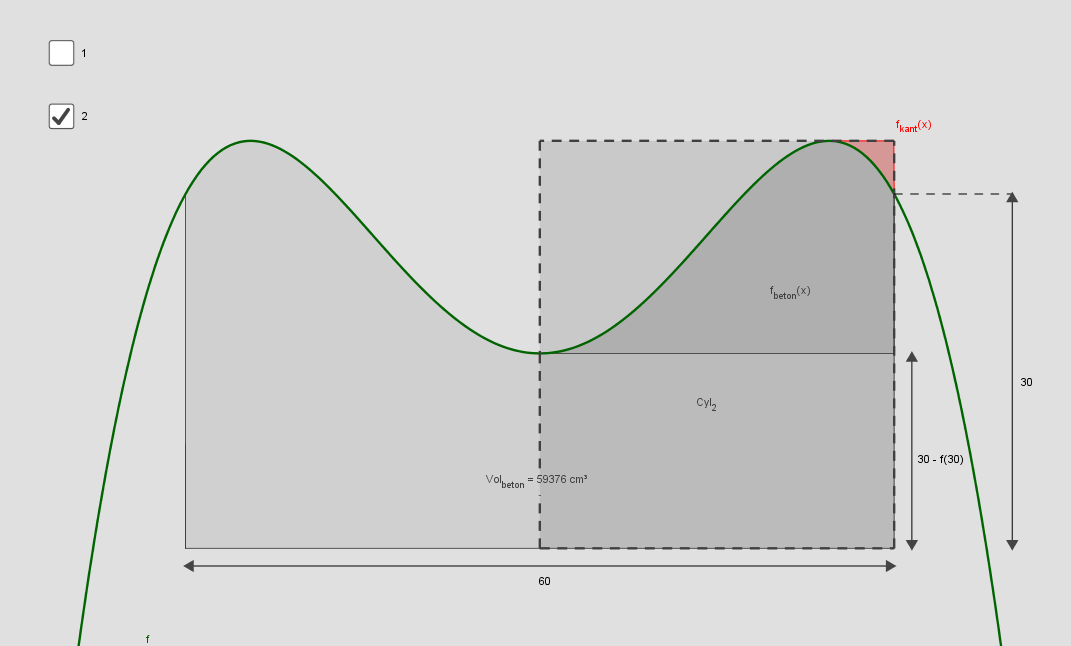
2. Betonmængde. En cylinder minus volumet af vasken minus volumet af kanten:

$\begin{align*} Cyl_{2}(x) &= f(x_1)+\left |f(30)-30\right |\;,\;0\leq x\leq 30 \\ Vol_{beton} &= 2\pi\cdot \left (\int_{0}^{30}x\cdot Cyl_{2}(x)\,dx -\int_{0}^{x_1}x\cdot f(x)\,dx -\int_{x_1}^{30}x\cdot f(x)\,dx\right ) \\ &= 2\pi\cdot \left (\int_{0}^{30}x\cdot Cyl_{2}(x)\,dx -\int_{0}^{30}x\cdot f(x)\,dx\right ) \\ &= 2\pi\cdot 9450 \approx 59376 \,(cm^3) \end{align*}$

Vedhæftet fil:A_M_086_2 - Vask, omdr.- legeme_DeepOcean.png

Brugbart svar (0)

Svar #17
09. februar 2020 af ringstedLC

#16: Rettelse.

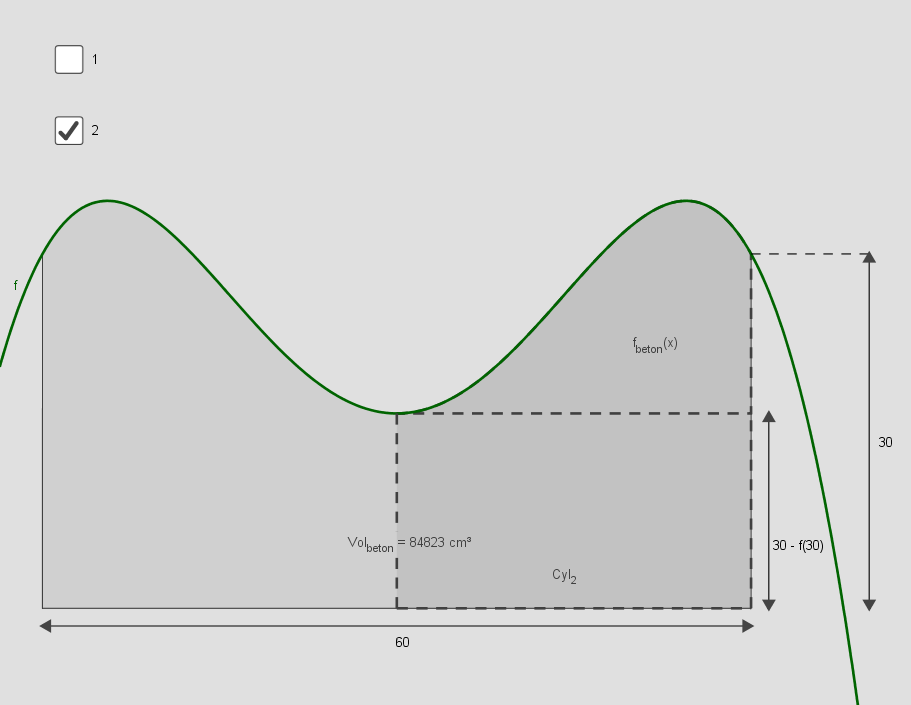
2. Betonmængde: En cylinder plus volumet af omdrejningslegemet af f_beton(x):

$\begin{align*} Cyl_2(x) &= {\color{Red} \left | 30-f(30) \right |}\;,\;0\leq x\leq 30 \\ Vol_{beton} &= 2\pi\cdot \left (\int_{0}^{30}x\cdot Cyl_2(x)\,dx \;{\color{Red} +}\int_{0}^{30}x\cdot f(x)\,dx\right ) \\ &= 2\pi\cdot {\color{Red} 13500}\approx 84823\;(cm^3) \end{align*}$

Vedhæftet fil:A_M_086_2 - Vask, omdr.- legeme_DeepOcean.png

Skriv et svar til: Integral

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.