Matematik

Væksthastighed

12. februar 2020 af NW12 - Niveau: B-niveau

Halløj. Nogen som kan hjælpe med denne her opgave? Jeg løser opgaven i TI-Nspire. Tak på forhånd:)

Vedhæftet fil: øælkjhg.png

Brugbart svar (0)

Svar #1
12. februar 2020 af mathon

Brugbart svar (0)

Svar #2
12. februar 2020 af mathon

$\small \begin{array}{llll} &f2(x):=\frac{\mathrm{d} }{\mathrm{d} x}(f1(x))\\\\&f3(x)=\frac{\mathrm{d} ^2}{\mathrm{d} x^2}(f1(x))\\\\\\\textup{maksimal v\ae ksthastighed}\\\textup{kr\ae ver:}&f3(x)=0 \end{array}$

Svar #3
12. februar 2020 af NW12

Hvordan det? Kan du give en forklaring på dette?:)

Brugbart svar (0)

Svar #4
12. februar 2020 af ringstedLC

#3:

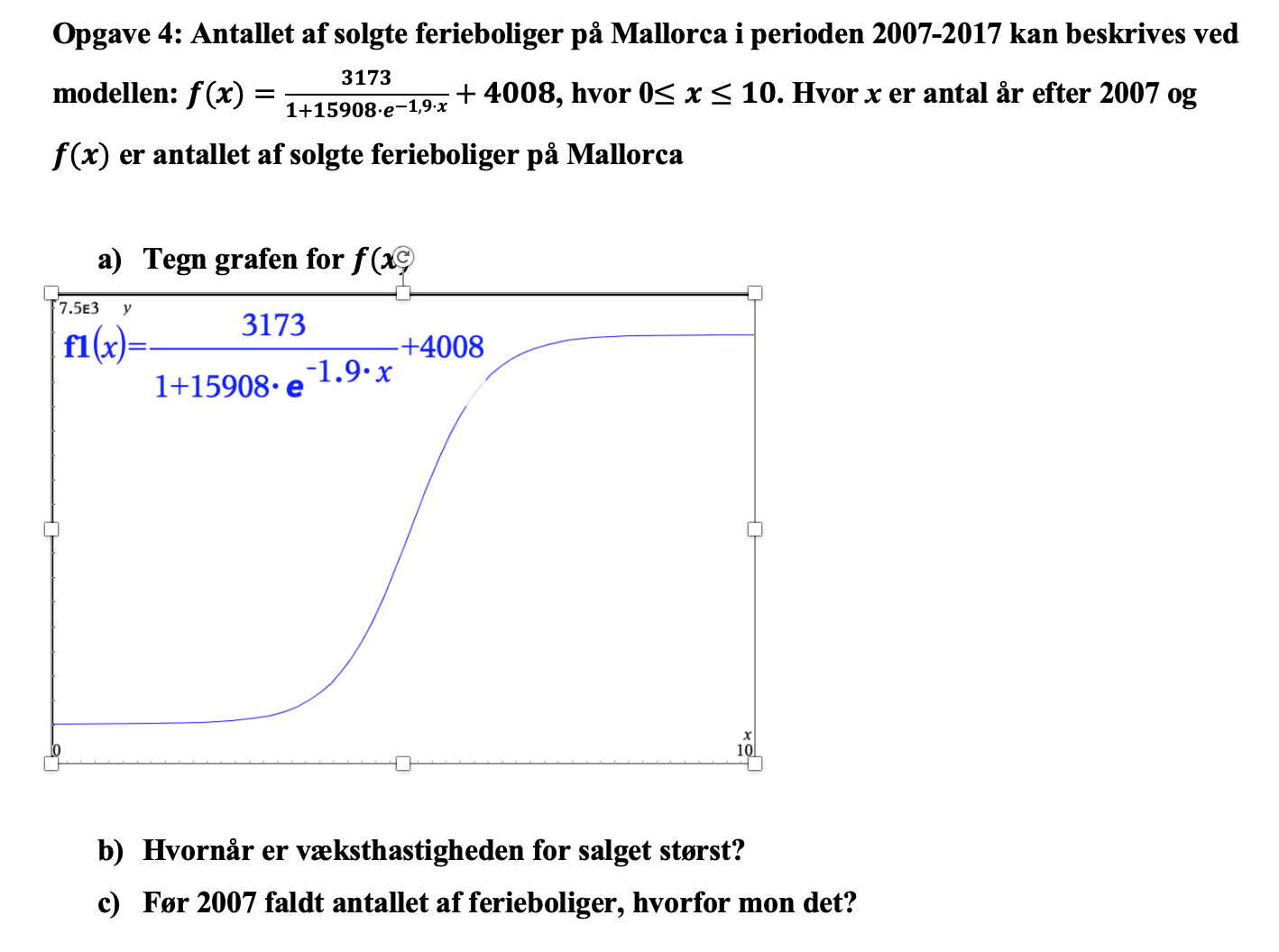
f1(x) = antal.

f2(x) = f1'(x) = vækst.

f3(x) = f1''(x) = f2'(x) = væksthastighed.

Svar #5
13. februar 2020 af NW12

Hvorfor er der så et f3(x)? Forstår heller ikke det der d² og dx²?

Brugbart svar (0)

Svar #6
13. februar 2020 af ringstedLC

$\begin{align*} \frac{d}{dx}f1(x) &= f1'(x) \\ \frac{d^2}{dx^2}f1(x) &= f1''(x) \end{align*}$

Svar #7
13. februar 2020 af NW12

Sorry. Men det giver altså stadig ingen mening... hvordan skal jeg få et tal ud af det?

Brugbart svar (0)

Svar #8
13. februar 2020 af 101214 (Slettet)

Når du differentiere f(x) kan du bruge den til at finde væksten af antallet af ferieboliger, men hvis du differentire den igen finder du væksthastigheden, her kan du løse den for maksimum.

altså først differentier f(x) to gange og derefter løs for 0, f''(x)=0 her kan du finde monotoniforhold for at se om det er maksimum eller minimum.

Brugbart svar (0)

Svar #9
14. februar 2020 af mathon

...altså først differentier f(x) to gange og derefter løs for f''(x) = 0. Fortegnsvariationen for f''(x) bestemmer
monotoniintervalgrænserne for f'(x), som er væksthastigheden for f(x).

Når fortegnsvariationen for f''(x)
i en lille omegn af et ekstremumspunkt er:
+ 0 - har f'(x) - væksthastigheden - lokalt/globalt maksimum

- 0 + har f'(x) - væksthastigheden - lokalt/globalt minimum

Svar #10
14. februar 2020 af NW12

Okay, takker:)

Skriv et svar til: Væksthastighed

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.