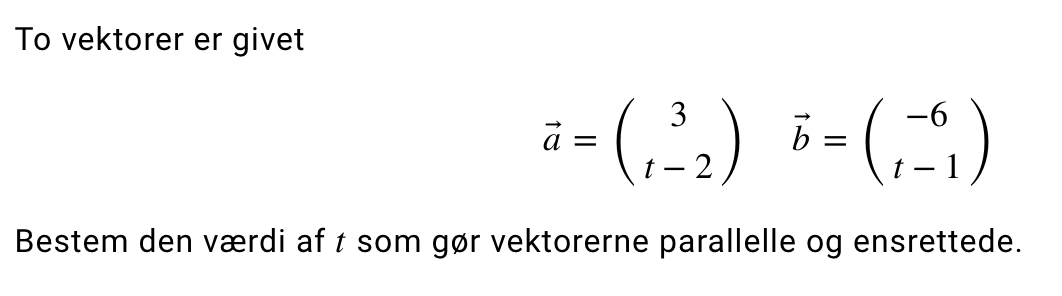Matematik

Vektorer

02. april 2020 af Monica12345 - Niveau: A-niveau

Hej

Jeg har brug for hjælp til at bestemme t (se nedenstående billede)

Jeg tænker, at man kan bruge reglen om, at vektor a = k * vektor b, men jeg ved ikke lige, hvordan jeg skal komme videre og finde t, når vektorerne både skal være parallelle og ensrettede.

Håber at nogle kan hjælpe mig!

Vedhæftet fil: Skærmbillede 2020-04-02 kl. 20.09.47.png

Brugbart svar (0)

Svar #1
02. april 2020 af mathon

For parallelle vektorer er determinanten lig med 0.

For ortogonale vektorer er prikproduktet lig med 0.

Beregn $t$ ud fra ovenstående forudsætninger.

Svar #2
02. april 2020 af Monica12345

Tak, vil det så sige, at t=15/9=1,67?

Brugbart svar (0)

Svar #3
02. april 2020 af mathon

Brugbart svar (0)

Svar #4
02. april 2020 af mathon

#2
Nej.

Brugbart svar (0)

Svar #5
02. april 2020 af Mathias7878

Som skrevet i #1 skal du løse

$\overrightarrow{a} \cdot \overrightarrow{b} = a_1 \cdot b_1 + a_2 \cdot b_2 = 0$

$det(\overrightarrow{a}, \overrightarrow{b}) = a_1b_2-a_2b_1 = 0$

- - -

Brugbart svar (0)

Svar #6
07. april 2020 af ringstedLC

Opgaven er lidt tvetydig. Måske er det en indlagt fælde.

For parallelle vektorer:

$\begin{align*} \vec{a}\parallel \vec{b}\Rightarrow det\,(\vec{a}\,,\vec{b}) &= 0 \\ a_1\, b_2-a_2\, b_1 &= 0 \\ a_1\, b_2 &= a_2\, b_1 \\ 3\cdot (t-1) &= (t-2)\cdot (-6) \\ t-1 &= -2\, t+4 \\ t &= \tfrac{5}{3} \end{align*}$

eller:

$\begin{align*} \vec{a} \parallel \vec{b} \Rightarrow \vec{a} &= k\cdot \vec{b}\;,\;k\neq 0 \\ \begin{pmatrix}3\\t-2 \end{pmatrix} &= k\cdot \begin{pmatrix}-6\\t-1\end{pmatrix} \\ 3=k\cdot (-6) &\, \wedge t-2=k\cdot (t-1) \\ k=-\tfrac{1}{2} &\, \wedge k=\tfrac{t\,-\,2}{t\,-\,1} \\ -\tfrac{1}{2} &=\tfrac{t\,-\,2}{t\,-\,1} \Rightarrow t=\tfrac{5}{3} \\ k &= -\tfrac{1}{2} \Rightarrow \vec{a} \rightleftarrows \vec{b} \end{align*}$

For ensrettede vektorer (som selvfølgelig også er parallelle):

$\begin{align*} \vec{a} \rightrightarrows \vec{b}\Rightarrow \vec{a} &= k \cdot \vec{b}\;,\;k>0 \\ \begin{pmatrix}3\\t-2\end{pmatrix} &= k \cdot \begin{pmatrix}-6\\t-1\end{pmatrix} \\ 3=k\cdot (-6) &\, \wedge t-2=k\cdot (t-1) \\ k=-\tfrac{1}{2} &\, \wedge k=\tfrac{t\,-\,2}{t\,-\,1} \\ k &\, \in \varnothing \Rightarrow \vec{a} \text{ og } \vec{b} \text{ er ikke ensrettede} \Rightarrow t \in \varnothing \end{align*}$

t kan bestemmes, så vektorerne er parallelle, men modsatrettede.

Skriv et svar til: Vektorer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.