Panserformlen bevis

Det kan du godt; men det er lidt overflødig da integralet på højre side jo selv indeholder en ubestemt konstant

Men er lidt i tvivl om hvorfor jeg har trukket det fra. Nogen steder skriver de nemlig med et plus (se vedhæftede i denne besked), er det så forkert?

Min forklaring jeg har skrevet til at jeg trækker den fra er: 

- Hvis vi tager stamfunktionen på begge sider, ved vi at de to stamfunktioner er ens på nær en konstant c. 

Forstår ikke helt hvorfor man godt må trække konstanten c fra...?

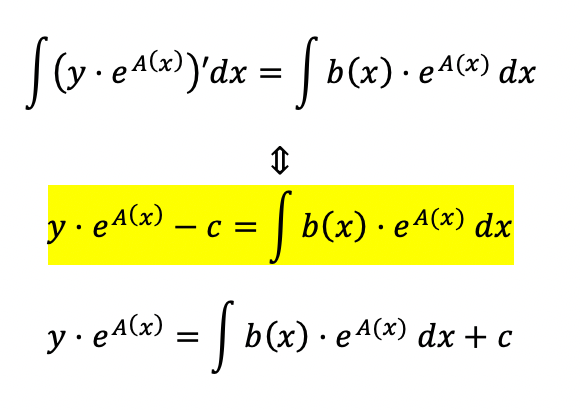
Såvel som  er stamfunktioner til , og så adskiller de sig bare fra hinanden med en konstant.

Om du lægger denne konstant til den ene eller den anden er ligegyldigt. Det er også ligegyldigt, om du kalder konstanten c eller -c, da du i begge tilfælde får alle reelle tal med (G(x) = F(x) + k ⇔ F(x) = G(x) - k).
Her har man så valgt at skrive F(x) = G(x) - c, så man senere får + c på højresiden (det er pænere).

Du kunne også have sagt + k, og når du så i næste trin fik - k på højresiden, kunne du omdøbe -k til c.

Så man kan forstå det som at venstresiden i det gule udtryk angiver stamfunktionen og højresiden angiver den fuldstændige løsning, da man lægger en konstant til?

#3: 

- man kan vel ikke skrive G(x)+k?

 

Det er bare en ubestemt konstant som både kan være positiv og negativ så hvad enten du skriver +c eller -c er ligegyldig. Du får alle muligheder med

Begge sider er den fuldstændige løsning - de er jo ens. Du kan ikke tale om stamfunktionen - der er jo uendeligt mange stamfunktioner.

#4      - man kan vel ikke skrive G(x)+k?

Jeg er ikke sikker på, jeg forstår, hvad du mener. Om du skriver G(x) = F(x) + k eller F(x) = G(x) + k er ligegyldigt. k vil bare have modsat fortegn i de to tilfælde, og k skal jo gennemløbe alle reelle tal (positive som negative) for at få samtlige løsninger.

#5: 

Tusind tak, okay så for at være helt sikker, ville forklaringen fra linje 1 til 2 så bare være: 

Når vi integrerer vores udtryk på venstresiden vil vi få en fuldstændig løsning ved at trække konstanten c fra,  højresiden angiver en stamfunktion... - føler ikke jeg forstå det helt rigtigt, hvordan skal det forklares...?
 

#2 
                                              
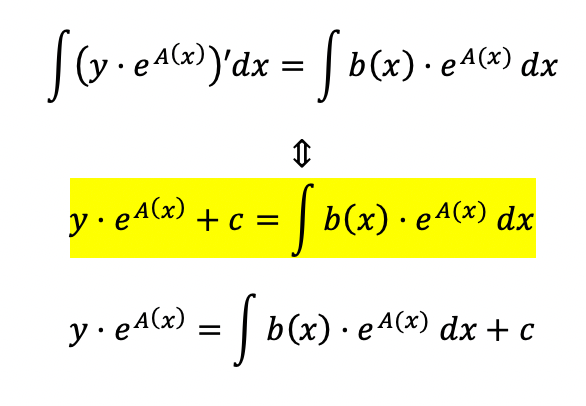
Sidste linje er forkert, da der skulle - c på højresiden, men ...
Hvis vi nu i den gule linje kalder konstanten k i stedet for c, så får vi i sidste linje - k på højresiden.
Så laver vi "barnedåb" og sætter c = -k og så står der det, vi gerne ville have.
Din ide med at kalde konstanten -c i linje 2 er mindst lige så god, og så undgår du fortegnsfejlen i sidste linje.

Men hvorfor er det okay at kalde konstanten for -c? For hvis man nu sagde at kosntanten var 5, så vil den jo få et modsat fortegn dvs. blive -5, hvis jeg indsatte det, og så er konstanten jo ikke længere 5...?

#7 Hellere:
"Når vi integrerer vores udtryk på venstresiden skal vi bestemme en stamfunktion og lægge en konstant til.
 er stamfunktion til , og konstanten kalder jeg -c, hvor c ∈ R." 

NB! At integrere en funktion betyder at bestemme samtlige stamfunktioner til funktionen.
 

#7:
Okay tak, giver mere mening. Men synes bare altid man har fået afvide, at man skal lægge en integrationskonstant til og ikke trække en fra. Kan godt se, at man så opnår at der står +c på højresiden, men man har det jo så bare ikke på venstresiden...

#9 For den enkelte stamfunktion har det selvfølgelig betydning, om der står + 5 eller - 5, men k bestemmes jo ud fra den enkelte funktion, ikke omvendt.

Hvis vi tager et eksempel med den klassiske opgave:
f(x) = 3x² + 4x +1. Bestem den stamfunktion, hvis graf går gennem P(1,7)
F(x) = x³ + 2x² + x + k,  F(1) = 7 ⇔ 4 + k = 7 ⇔ k = 3, så F(x) = x³ + 2x² + x + 3
G(x) = x³ + 2x² + x - k,  G(1) = 7 ⇔ 4 - k = 7 ⇔ k = -3, så G(x) = x³ + 2x² + x + 3

#11 Du har jo også lagt en integrationskonstant til - du har lagt -c til.
Det er ligegyldigt, hvad du kalder  konstanten, bare den gennemløber samtlige reelle tal. Du kunne for den sags skyld kalde den 735k eller k³ eller 3k-4, men det kan være lidt svært at få øje på det smarte i det.

#9

Okay eksemplet gav mega god mening, tak! Så man kan vel sige at trække -c eller ligge c til giver den samme konstant når man integrerer, da man jo skal isolerer for c ved at indsætte et punkt.