Matematik

Optimering af cirkulær cylinder

19. juni 2020 af DeepOcean - Niveau: A-niveau

Hej Alle.

Jeg sidder med den spændende opgave om optimering og har vist brug for hjælpe.

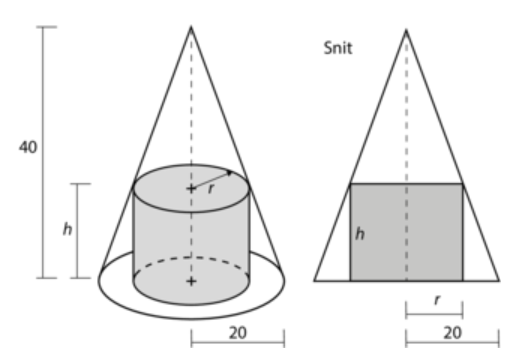
Der er indskrevet en cirkulær cylinder i en kegle som vist på figuren. Der er tillige vist et snit gennem konstruktionen. Alle mål er i centimeter.

Bestem de værdier for r og h, der giver det størst mulige volumen af cylinderen.?

Figuren vedhæftes

Vedhæftet fil: Cylinder.PNG

Brugbart svar (0)

Svar #1
19. juni 2020 af Soeffi

#0. Se evt. en af følgende videoer: https://www.youtube.com/results?search_query=cylinder+in+cone.

Brugbart svar (0)

Svar #2
19. juni 2020 af mathon

Brugbart svar (1)

Svar #3
19. juni 2020 af mathon

Benyt ensvinklede trekanter.

Brugbart svar (1)

Svar #4
19. juni 2020 af mathon

$\small \small \begin{array}{lllll}& \frac{40}{20}=\frac{40-h}{r}\\\\ \textup{hvoraf:}&2r=40-h\\\\& h=\left (40-2r \right )\\\\ \textup{cylinderrumfang:}&V_{\textup{cyl}}(r)=h\cdot \pi\cdot r^2\\\\& V_{\textup{cyl}}(r)=(40-2r)\cdot \pi\cdot r^2\\\\& V_{\textup{cyl}}(r)=-2\pi\cdot r^3+40\pi\cdot r^2\\\\& V_{\textup{cyl}}{}'(r)=-6\pi\cdot r^2+80\pi \cdot r=-6\pi r\left ( r-\frac{80}{6} \right )\\\\ \textup{Maksimum kr\ae ver bl.a.:}&V_{\textup{cyl}}{}'(r)=-6\pi r\left ( r-\frac{80}{6} \right )=0\textup{ ..}._\textup{{osv}}\textup{ ...} \end{array}$

Brugbart svar (1)

Svar #5
19. juni 2020 af mathon

Cirkulær cylinder er en pleonasme.

Svar #6
19. juni 2020 af DeepOcean

Mange tak for god forklaring.

Skriv et svar til: Optimering af cirkulær cylinder

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.