Beregning af afstand med bredde og længdegrader

Der mangler oplysning om N/S og Ø/V på bredde- og længdegraderne.

Hvis A og B ligger på fx den nordlige halvkugle og har østlige længdegrader:

Hej og tak for svar - Jeg formoder begge steder ligger på den nordlige halvkugle selvom afstanden er 4,314 km

Jeg har regnet på afstandformlerne både i grader og km og kom frem til (formel 1)  = 38,096596 grader og afstanden i km er så grader*omkredsen / 360 - i dette tilfælde er omkredsen oplyst til at være 40.840,7045 og grader er oplyst til at være 38,03211355 forskellen fra min egen beregning til den oplyste er minimal

Den oplyste: 38,03211355*40840,7045/360 = 4.314,60 km

Min egen beregning : 38,096596*40840,7045/360 = 4321,92 km.

Jeg har brugt begge de formler du skriver. - Det var egentligt også mere hvordan man kommer frem til graderne med de henholdsvis X,Y,Z (A)  og X,Y,Z (B) jvf. oplysningerne i min første forespørgsenl hvor der ern nogle andre formler der bruges.   mvh Tonny

Jeg har regnet på afstandformlerne både i grader og km og kom frem til (formel 1)  = 38,096596 grader 

Jeg har brugt begge de formler du skriver. - Det var egentligt også mere hvordan man kommer frem til graderne med de henholdsvis X,Y,Z (A)  og X,Y,Z (B) jvf. oplysningerne i min første forespørgsenl hvor der ern nogle andre formler der bruges.   mvh Tonny

Den sidste er blot en omskrivning af din egen.

Det virker lidt underligt, at facit er opgivet med så mange decimaler, men du burde kunne "ramme" det bedre med et tilstrækkeligt antal decimaler; fx fem.

Læs mere fx på: https://da.wikipedia.org/wiki/Sf%C3%A6risk_trigonometri

Det kan være bekvemt at få vinklen, der spænder over storcirkelbuen, ud i radianer.
For at få længden af buen ganges med kuglens radius.

Super kanon Tak for svar - rigtigt godt - nu kan jeg regne videre på alle formlerne - jeg er ved at få fat i det men læser også meget på lektien og med dine gode råd er det efterhånden ved at være inde på min lystavle - Jeg synes sfærisk trigonimetri er spændende men også i den svære ende.

Hav en dejlig dag fra Tonny

Hej igen - Sorry men jeg så første du havde skrevet igen omkring buelængden. Jeg har brugt formlen for cirkelafsnit  som hedder : diameter*Pi()/360/vinklen - idette tilfælde : 13000*Pi())/(360/38,03) = 4314,367 som svarer til "rejsen"  MEN du må meget gerne fortælle mig om det kan gøres anderledes med et eksempel jvf. omstående - På forhånd tak fra Tonny

For at kunne beregne den korteste vej, mellem to punkter, langs en kugleflade, benyttes
en sfærisk polartrekant. I en sfærisk polartrekant er den ene vinkel, C, beliggende i en af polerne,
her i regneeksemplet, Nordpolen, N.
Polens modstående side, c, er den storcirkelbuelængde, vi skal finde, der er afstanden.
Fra N ned til 21º ø.l. 34º n.b. er storcirkelbuen 90º - 34º = 56º
Fra N ned til 69º ø.l. 45º n.b. er storcirkelbuen 90º - 45º = 45º
Polarvinklen, C, er  69º - 21º = 48º
Nu har vi materialet i orden til at kunne indsætte i den sfæriske cos-relation:
        cos c = cos a · cos b + sin a · sin b · cos C
Til sidst findes c, som mest bekvemt angives i radianer, og som ganges med kuglens radius.    

Hej Capion . tusinde Tak for oplysningerne - nu har jeg beregnet afstanden både med 34 grader og 45 grader og forskellen mellem længdegraderne på 48 grader MEN jeg har også beregnet afstanden med 56 og 45 grader samt forskellen på længdegraderne og derved fundet graden 38,03 som jeg har ganges med omkredsen og delt med 360 og således fundet afstanden på de 4.314,60 km - super indtil videre - jeg fik så imidlertid en anden formel fra et ander flinkt menneske som beregner vinkel (38,03) med denne formel

kvrod(2)/2*(sin(34)+cos(34)*cos(48))

DeT hele i radianer) begge formler virker altså - jeg har så prøvet med andre afstande og så går det galt med formlen med kvadratroden - jeg må øve mig videre indtil det lykkedes med begge formler - men tusinde tak for din hjælp - hav en fortsat god dag fra Tonny

PS - har du et godt råd mht til kvadratrodsformlen hører jeg meget gerne herom) 

Da både
   
og
 
kan højresiden indsættes som faktor i stedet for sin eller cos af vinklen.
Men kvadratrodsformlen gælder naturligvis kun for denne vinkel.

Sorry - jeg mente at jeg fik den rigtige grad og afstand med 56-45-48 i cos-relationen og den rigtige afstand med kvadratrodformelen 34,34,48 - begge gav resultatet 38,03 grader

Super tak - jeg regner videre - jeg må erkende at sfærisk trigonometri ligger i den hardcore ende af geometrien.

Fortsat god dag fra Tonny

Skal vi fra København til New York skal vi, ad den korteste vej, flyve i nord-vestlig retning og overflyve det nordligste af Skotland, til trods for at New York ligger sydligere end København.  (ca. 6196 km)
Man kan kalde det for flyvningens paradoks, - indtil man ved alt om storcirkler. :)

Det er rigtigt-  jeg har bemærket når jeg tjekker afstande ex fra københavn til New York så flyver man i en bue - men det er velsagtens grundet jorden rotation at man planlægger kursen til bestemmelssteden inden afgangen?? mvh Tonny

De gamle grækere fik den tanke, at hoppede man tilstrækkeligt højt op i luften, ville man lande i et
punkt, der lå lidt vest for det punkt, man var hoppet fra.
Det ville være en fristende tanke at kunne stige op i en helikopter, blive hængende tilstrækkeligt
længe i luften, og derefter lande efter et stykke tid.

ha ha - ja det kunne være bravt: men hvis man kunne hænge længe nok i luften uden jordkontakt så burde man næsten kunne se jorden dreje rundt (øh!!) jordens rotation ved vores breddegrad er trods alt 940 km i timen rundt regnet - hvorom alting er så kan vi takke de gamle grækere for meget - mit store idol er Arhcimedes - hyggeligt og ikke mindst interessant at tale med dig Caption !  god hilsen fra Tonny

Hej Capion

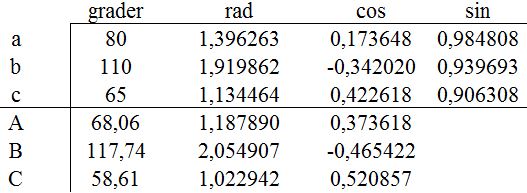
I forlængelse af arbejdet med afstande som jeg efterhånden har fået godt tjek på - jeg har lavet flere regnestykker der går op hvilket er godt. Jeg sidder nu og arbejder med vinklerne Cos A Cos B og Cos C udfra følgende oplysninger  med de 3 sider som er a= 80° b= 110° og c=65° som jeg har opstllet i følgende formler:

Cos A = cos(80)-cos(110)*cos(65) / sin(110)*sin(65) - radianen skal blive 0,7362 og vinkel  = 21,93 grader - her rammer jeg 0,3736 som giver sinus til vinkel men ikke cos (spooky)

Cos B = (med de samme sider a,b,c)  cos(b)-cos(a)*cos(c) / sin(a)*sin(c) - radianen skal blive -0,4654 og vinklen 117,74 grader og her rammer jeg klokkerent  altså cosinus til vinklen 

Cos C= cos(c)-cos(a)*cos(b)/sin(a)*sin(b) - radianen skal blive 0,5400 og vinklen  57,51 grader men her får jeg en radian på 0,5208 og en vinkel på 58,61 grader. Jeg har prøvet og prøvet men AK - det mislykkedes - Kan jeg gøre noget forkert? Formlerne passer jo - jeg har tripple tjekket - måske du kan give et råd - underligt jeg rammer Cos B klokkerent men ikke de andre 2 med nøjagtigt samme opstilling. måske et godt råd? - bedste hilsner fra Tonny

.

Hej caption og tusinde tak.

 Det giver mig da noget at arbejde med - hav en skøn dag fra Tonny

Hej igen Cation

Så er der tjek på det  - jeg kan nu regne både sider og vinkler ud med cosrelationerne og er igang med sinusrelationerne - Det er dælme spændende trigonometri specielt når man er begyndt at fatte det - tusinde tak for din store hjælp og hav en fortsat god dag fra Tonny