Vektorer i rummet

Bestem to ikke-parallelle retningsvektorer for planen hvori P ligger samt et punkt i planen.
Du må i formelsamlingen kunne se, hvordan parameterfremstillingen nedskrives.
Der er to parametre, én for hver af retningsvektorerne.
 

Bestem fire vektorer, der forbinder punkterne. Hvis de parvis er parallelle og lige lange, må punkterne danne et parallellogram.

Arealet er absolutte (numeriske) værdi af determinanten.

#2 Man kan kun tage determinanten af en kvadratisk matrix.

Du mener nok at arealet er den absolutte værdi af krydsproduktet.

#2: Tak for rettelsen. Dog vil jeg mene, at det er længden af krydsproduktet.

#3 Rettelse:

Du mener nok at arealet er den absolutte værdi af krydsproduktet.

Du mener nok at arealet er den længden af krydsproduktet.

#4 Du har ret.

Arealet er kvadratroden af determinanten af matricen ganget sin egen transponerede.

hej
Et parallelogram er en firkant, hvor modstående vinkler er ens
så vinkel to vektoer BA og BD, det skal være lige med vinkel  of CD og CA
jeg fik svar på 0.70166 begge vinkel så det var samme vinkel så de er et parallelogram

...eller 
              forudsætningen for et parallellogram
              er bl.a.
                              

super:) , tak 

I et sædvanligt (x, y, z)-koordinatsystem i rummet betragtes punkterne A = (1,1,1), B = (3,0,0), C = (0,4,3) og D = (2,3,2).

a) Vis at de fire punkter udspænder et parallelogram P , opstil en parameterfrem- stilling for P , og bestem arealet af P .

For et vilka °rligt k > 0 betragtes vektoren v = (2, −1, k) .

b)  Bestem volumen (som funktion af k ) af den punktmængde der gennemfejes af P ,

na °r P parallelforskydesmed v.

spørgsmål b) 

Det er absolutværdien af determinanten af den 3x3 matrix du får af v=(2, −1, k), samt to ikke-parallelle sider af parallellogrammet, f.eks. AB og AC.

#8:

#8

hej
Et parallelogram er en firkant, hvor modstående vinkler er ens
så vinkel to vektoer BA og BD, det skal være lige med vinkel  of CD og CA
jeg fik svar på 0.70166 begge vinkel så det var samme vinkel så de er et parallelogram

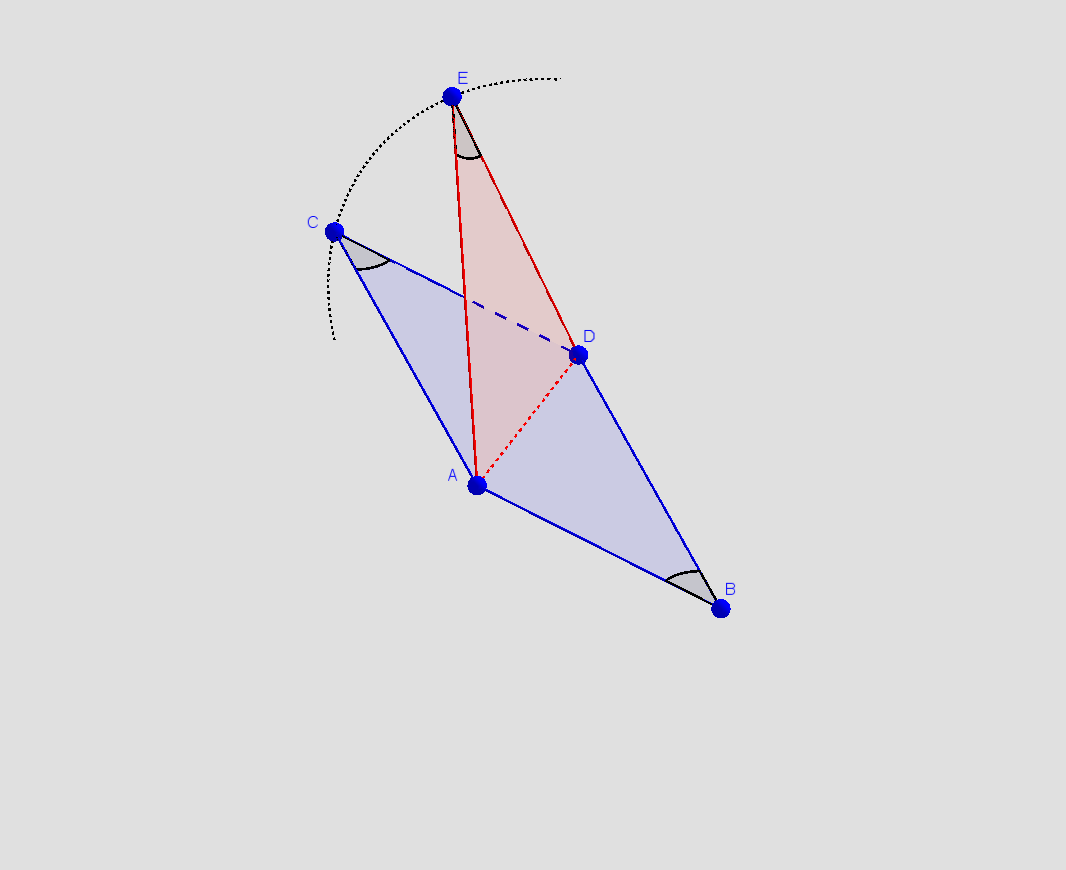
Dette kan kun bruges, når de fire punkter ligger i samme plan. På nedenstående figur er de tre vinkler også lige store.

Med metoderne i #2 og #9  vises, at punkterne ligger i samme plan.