Matematik
mat
25. oktober 2020 af
nana2020
-
Niveau: Universitet/Videregående
har brug for hjælp til d)
c) har jeg løst.
Svar #2
25. oktober 2020 af nana2020
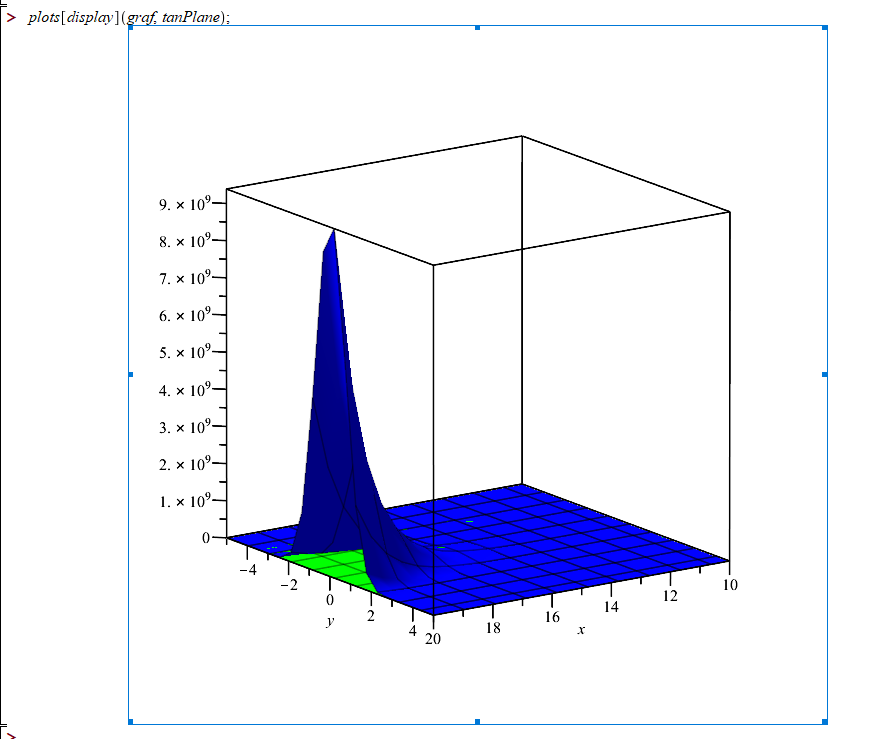
her er opgaven
Vedhæftet fil:Skærmbillede 2020-10-25 kl. 21.09.55.png
Svar #4
26. oktober 2020 af Cudex
har du fundet svaret? Kunne også godt tænke mig at vide det da vi sidder med samme opgave :)))
Skriv et svar til: mat
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.