Matematik

Integrale/Dobbelt Integrale

31. oktober 2020 af smklae (Slettet) - Niveau: Universitet/Videregående

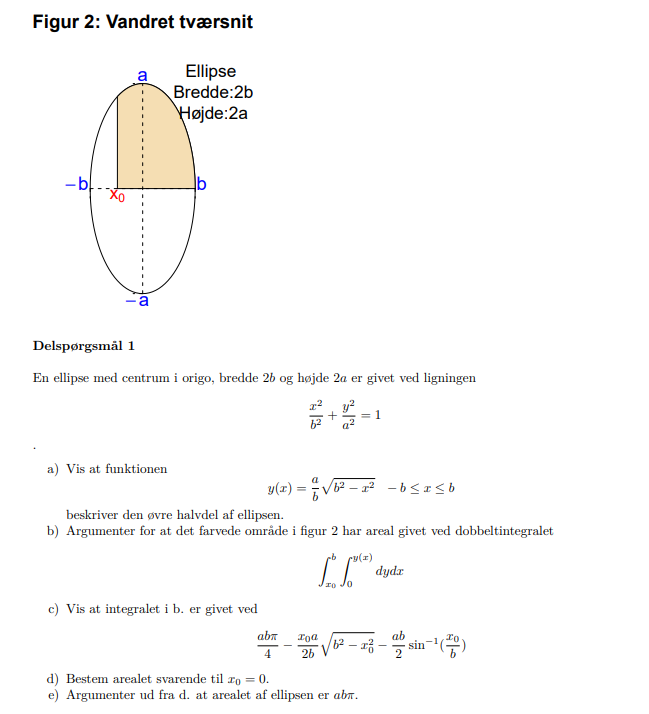
Hvordan skal jeg løse c)? Jeg sidder helt fast.

Vedhæftet fil: unknown (1).png

Brugbart svar (0)

Svar #1
31. oktober 2020 af Soeffi

#0.

Brugbart svar (1)

Svar #2
31. oktober 2020 af Soeffi

#0. c)

$\int_{x_0}^{b} \int_{0}^{y(x)}dydx=\int_{x_0}^{b} \int_{0}^{\frac{a}{b}\sqrt{b^2-x^2}}dydx=\int_{x_0}^{b}\left [ y \right ]_{0}^{\frac{a}{b}\sqrt{b^2-x^2}}dx=$

$\frac{a}{b}\cdot \int_{x_0}^{b}\left ( \sqrt{b^2-x^2} \right )dx=\frac{a}{2b} \cdot \left [b^2\cdot sin^{-1}(\frac{x}{b})+x \cdot \sqrt{b^2-x^2} \right ]_{x_0}^{b}=$

$\frac{a}{2b} \cdot \left (b^2\cdot sin^{-1}(\frac{b}{b})+b \cdot \sqrt{b^2-b^2}-b^2\cdot sin^{-1}(\frac{x_0}{b})-x_0 \cdot \sqrt{b^2-x_0^2} \right )=$

${\color{Blue} \frac{ab \pi }{4}-\frac{x_0a}{2b} \cdot \sqrt{b^2-x_0^2}-\frac{ab}{2} \cdot sin^{-1}(\frac{x_0}{b})}$

Skriv et svar til: Integrale/Dobbelt Integrale

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.