Matematik
Harmonisk Svingning
Hej med Jer.
Har ved hæftet en opgave som jeg undre mig over.
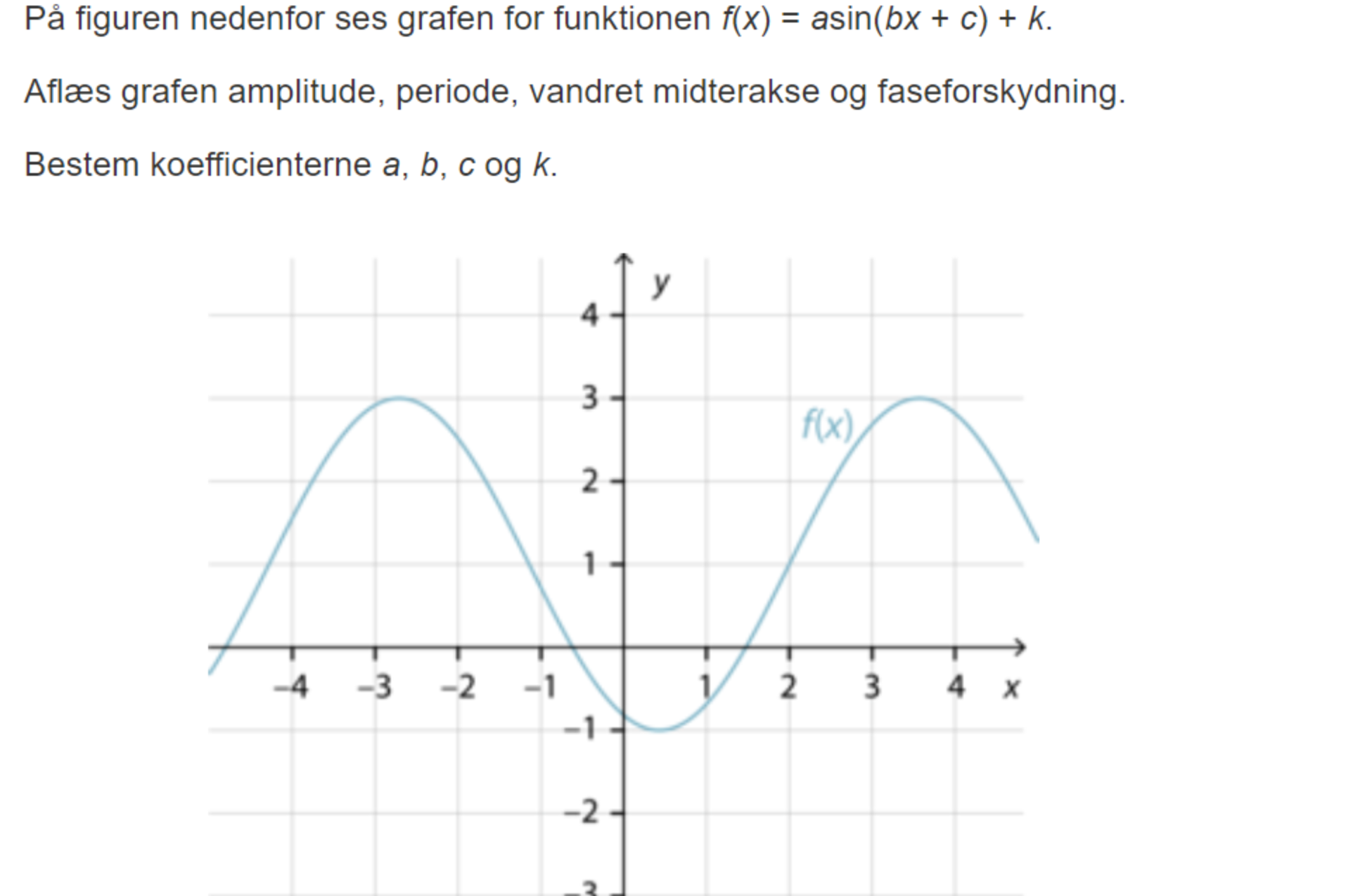
Undre mig lidt over denne opgave, hvordan koefficenterne a,b,c og k bestemmes.
mit bud er:
a=2
b=1
c=-2
k=-0.8
Svar #1
19. januar 2021 af Sveppalyf
Jeg vil mene at k skal være 1.
En sinuskurve svinger normalt symmetrisk op og ned omkring x-aksen, men denne graf svinger omkring den vandrette linje y=1. Dette svarer til at der bliver lagt 1 til funktionsværdien, så grafen bliver "løftet op". Så k=1.
Svar #3
19. januar 2021 af Sveppalyf
Den svinger mellem 3 og -1. Når den har amplituden 2, så stemmer det med at den svinger symmetrisk omkring 1. Altså 1+2 = 3 og 1-2 = -1.
Eller du kan bare tage gennemsnittet af 3 og -1.
Svar #6
20. januar 2021 af Sveppalyf
Faseforskydningen c udtrykker om grafen er forskudt mod venstre eller højre.
En almindelig sinusgraf starter i (0,0) og vokser så op mod sit første toppunkt i x = π/2. Vi skal finde det tilsvarende punkt på vores graf. Hvis du kigger på grafen i x=2, så har du at grafen lige har passeret sin midterakse og er på vej op mod sit første toppunkt. Så det punkt der normalt skulle ligge i x=0 ligger altså i x=2. Grafen er altså blevet forskubbet 2 mod højre, eller du kan betragte det som at grafen antager sine forskellige værdier med en forsinkelse på 2. Dette svarer til at der er blevet trukket 2 fra indmaden i sinusfunktionen. Atlså er c = -2.
Skriv et svar til: Harmonisk Svingning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.