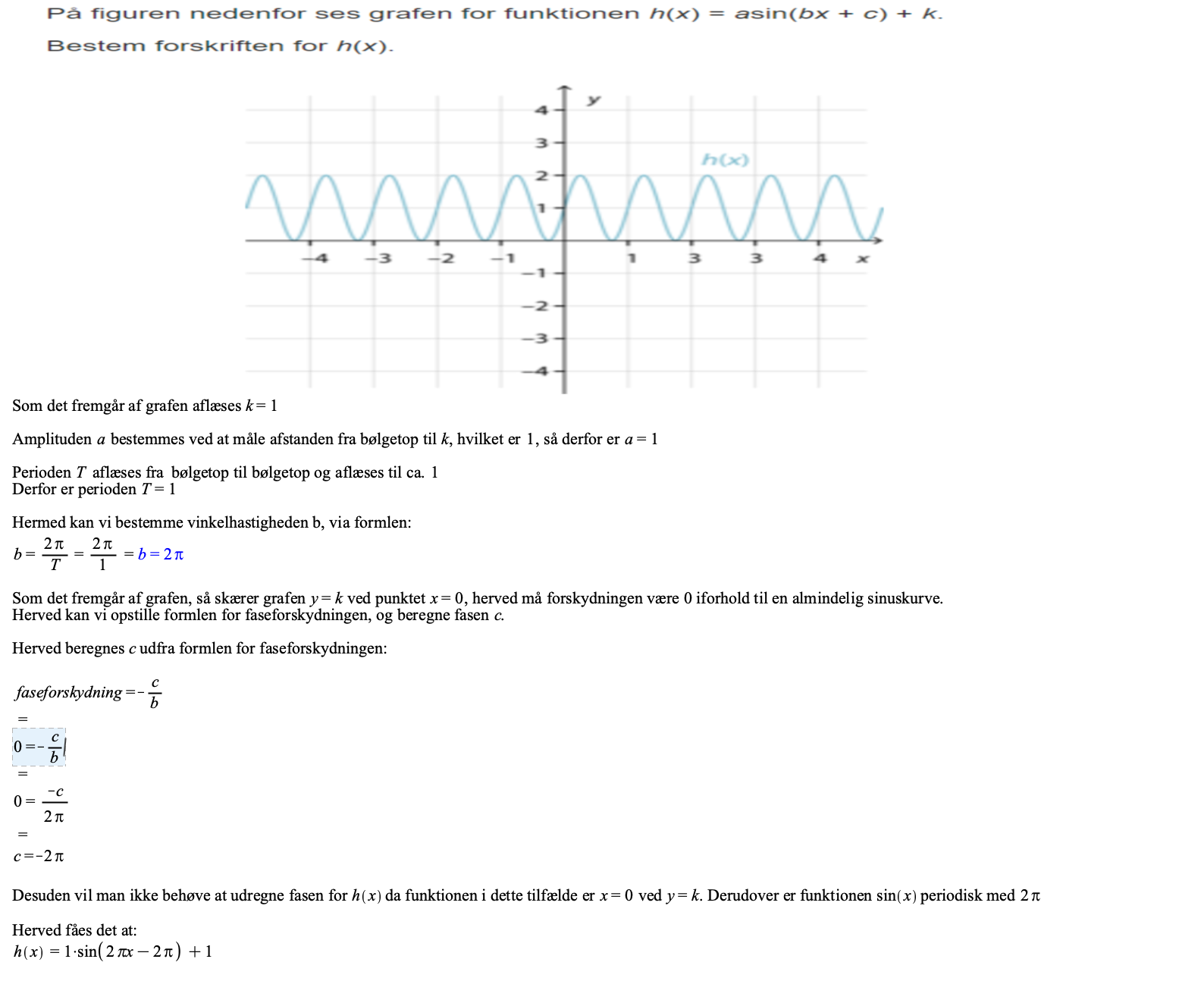
Matematik
Harmonisk Svingning
Hej.
Jeg søger feedback på mit svar til en forskrift, for er lidt usikker på den.
Har vedlagt alt.
Svar #1
23. januar 2021 af Eksperimentalfysikeren
Din beregning af c er forkert. 0 = -c/(2π) har løsningen c=0.
Svar #2
24. januar 2021 af ringstedLC
- Du aflæser værdier, de måles ikke.
- T: Kan ofte aflæses fra top til top, men uden "sikre punkter" for toppene, bør her bruges 2 halvperioder ved middelværdien.
- "... så skærer grafen y = k ved punktet x = 0..."; burde være "i punktet (0,1).
- Du beregner c (forkert desværre), hvorefter du argumenterer for, at det er unødvendigt.
- Forskriften er ikke reduceret færdig.
Svar #3
25. januar 2021 af dennis13434
Har vedlagt et alternativt svar
Vil det være bedre at gøre sådan?
Svar #5
25. januar 2021 af ringstedLC
#3: Bedre!.
Men du springer det med de "sikre punkter" over. Generelt skal man altid bruge skæringer mellem graf og gitter, når det kan lade sig gøre. Og man vælger så to punkter, der ligger så langt fra hinanden som muligt. Det øger nøjagtigheden af aflæsningen.
Se nærmere i https://www.studieportalen.dk/forums/thread.aspx?id=1951128, hvor problemet er nøjagtig det samme med bølgetoppene, hvorimod der nemt kan tælles et antal perioder ved at bruge middelværdien..
Bølgetoppenes x-værdi skærer ikke det lodrette gitter, men det gør derimod middelværdierne h(-4) og h(4). Tæl antallet af helperioder imellem disse skæringer og beregn så b udfra det næste gang.
#4: Det kan du godt, men det virker bare lidt mærkligt. Du starter opgaven med at aflæse k = 1, hvorfor så ikke bruge værdien.
Svar #6
28. januar 2021 af dennis13434
Fanger ikke helt tråden du har lagt ind
Kan du prøve eventuelt at vise hvordan du vil gripe opgaven an?
på forhånd tak
Svar #7
28. januar 2021 af ringstedLC
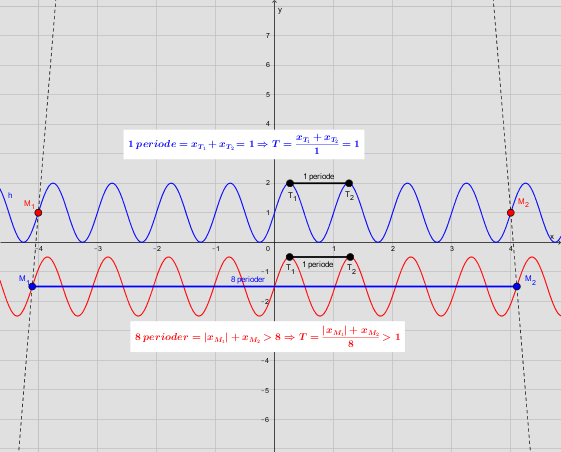
Den blå kurve er opgaven og den blå tekst er din aflæsning. Den røde kurve ville få den samme periode med din metode. Men som det ses, er det forkert og ville være opdaget med metoden i den røde tekst. Brug "sikre punkter", hvor det er muligt.
Svar #8
28. januar 2021 af dennis13434
Kan man istedet sige noget med:
"Jeg vælger at bestemme perioden ud fra y=k, hvilket den er i punktet (0,1) og (1,1), afstanden immelem disse punkter er 1, derfor er perioden T=1" ?
Svar #9
29. januar 2021 af ringstedLC
#8: Det er ret dårligt dansk og du mangler stadig noget af pointen i #5 og #7.
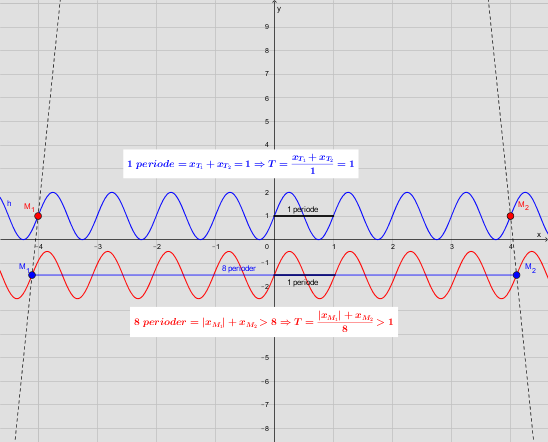
Den røde kurve aflæst med din metode og punkterne (0,k) og (1,k) giver en periode på 1. Men ved nærmere eftersyn ses det at perioden er større end 1. Igen; brug så mange perioder som muligt og vælg derfor punkterne (-4,1) og (4,1), tæl antal helperioder og divider afstanden med antallet. Det giver størst aflæsningsnøjagtighed.
Svar #11
29. januar 2021 af ringstedLC
#10: Korrekt og korrekt metode. Men se hvormeget eller rettere sagt hvorlidt den røde graf (T > 1) afviger, når der kun ses på én periode. Forskellen i T-værdi ganges jo op, når man ser på flere perioder.
Svar #12
29. januar 2021 af dennis13434
Hvis man ikke kan aflæse "sikre punkter", er første metode så ok?
Svar #13
30. januar 2021 af ringstedLC
Nej. Man udnytter bedst grafens udseende til bestemmelse af konstanter ved at bruge "hele" grafen i forhold til "hele" koordinatsystemet.
Svar #14
30. januar 2021 af dennis13434
Er dette svar på opgaven bedre?
Svar #16
30. januar 2021 af ringstedLC
#14

OK. Håber, at du har forstået min aflæsningsmetode og skulderklap for din vilje til at få opgaven besvaret.
Skriv et svar til: Harmonisk Svingning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.