Matematik

Vektorer

04. marts 2021 af Ceciliehansen02 - Niveau: A-niveau

Håber en vil hjælpe!

Vedhæftet fil: Skærmbillede 2021-03-04 kl. 11.23.18.png

Brugbart svar (0)

Svar #1
04. marts 2021 af mathon

Brugbart svar (0)

Svar #2
04. marts 2021 af AMelev

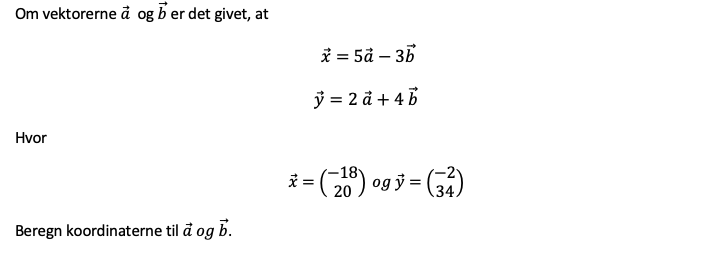
Gang første ligning igennem med 4 og anden med 3 og læg dem sammen, så kan du bestemme $\vec a$ .

Brugbart svar (1)

Svar #3
04. marts 2021 af mathon

$\small \small \begin{array}{lllll}& \vec{x}=5\cdot \begin{pmatrix} a_1\\a_2 \end{pmatrix}-3\cdot \begin{pmatrix} b_1\\b_2 \end{pmatrix}=\begin{pmatrix} -18\\20 \end{pmatrix}\\\\ \textup{hvoraf:}\\& \begin{array}{ll} I\textup{:}\quad 5a_1-3b_1=-18\\ II\textup{:}\quad \! \! \! 5a_2-3b_2=20 \end{array}\\\\\\& \vec{y}=2\cdot \begin{pmatrix} a_1\\ a_2 \end{pmatrix}+4\cdot \begin{pmatrix} b_1\\b_2 \end{pmatrix}=\begin{pmatrix} -2\\34 \end{pmatrix}\\\\ \textup{hvoraf:}\\& \begin{array}{ll} III\textup{:}\quad 2a_1+4b_1=-2\\ IV\textup{:}\quad \, 2a_2+4b_2=34 \end{array}\\\\\\& \begin{array}{ll} I\textup{:}\quad \, \, \, \, \, \, 5a_1-3b_1=-18\\ III\textup{:}\quad 2a_1+4b_1=-2 \end{array}\\\\\\& a_1=\frac{\begin{vmatrix} -18&-3\\ -2&4 \end{vmatrix}}{\begin{vmatrix} 5 & -3\\ 2& 4 \end{vmatrix}} \\\\\\& b_1=\frac{\begin{vmatrix} 5 & -18\\ 2&-2 \end{vmatrix}}{\begin{vmatrix} 5 &-3 \\ 2& 4 \end{vmatrix}} \end{array}$

Brugbart svar (1)

Svar #4
04. marts 2021 af mathon

$\small \small \begin{array}{llllll}& \begin{array}{ll} II\textup{:}\quad 5a_2-3b_2=20 \\ IV\textup{:}\quad \! \! 2a_2+4b_2=34 \end{array}\\\\\\& a_2=\frac{\begin{vmatrix} 20 &-3 \\ 34& 4 \end{vmatrix}}{\begin{vmatrix} 5 &-3 \\ 2& 4 \end{vmatrix}}\\\\\\& b_2=\frac{\begin{vmatrix} 5 &20 \\ 2& 34 \end{vmatrix}}{\begin{vmatrix} 5 &-3 \\ 2& 4 \end{vmatrix}} \end{array}$

Svar #5
04. marts 2021 af Ceciliehansen02

Tusind tusind tak for hjælpen. Er dette så svaret på opgaven, altså koordinaterne til vektor a og vektor b?

Brugbart svar (0)

Svar #6
04. marts 2021 af mathon

$\small \small \begin{array}{lllll} \overrightarrow{a}=\begin{pmatrix} a_1\\a_2 \end{pmatrix}&&&&\overrightarrow{b}=\begin{pmatrix} b_1\\b_2 \end{pmatrix} \end{array}$

Svar #7
04. marts 2021 af Ceciliehansen02

Mathon

Vil du måske hjælpe med denne opgave også?

Vedhæftet fil:Skærmbillede 2021-03-04 kl. 14.25.25.png

Brugbart svar (1)

Svar #8
04. marts 2021 af AMelev

#7 Husk kun én opgave pr. tråd, ellers bliver det noget roderi.
Bortset fra det, er det jo samme opgavetype som den foregående, så hvis du har lært noget af den hjælp, du har fået der, bør du selv kunne klare denne.

Alternativ metode, jf #2.
$\begin{Bmatrix} \vec x=5\vec a-3\vec b\\ \vec y=2\vec a+4\vec b \end{Bmatrix}\Leftrightarrow \begin{Bmatrix} 4\vec x=20\vec a-12\vec b\\ 3\vec y=6\vec a+12\vec b \end{Bmatrix}\Leftrightarrow \begin{Bmatrix} 4\vec x+3\vec y=26\vec a\\ \frac{1}{4} \cdot (\vec y-2\vec a)=\vec b \end{Bmatrix}\Leftrightarrow \begin{Bmatrix} 4\vec x+3\vec y=26\vec a\\ \frac{1}{4} \cdot (\vec y-2\vec a)=\vec b \end{Bmatrix}\Leftrightarrow$

$\begin{Bmatrix} \frac{1}{26}\cdot 4\left (\vec x+3\vec y \right )=\vec a\\ \frac{1}{4} \cdot (\vec y-2\vec a)=\vec b \end{Bmatrix}\overset{indsaet}{\Leftrightarrow} \begin{Bmatrix} .......=\vec a\\ .......=\vec b \end{Bmatrix}$

Metoden (lige store koefficienters metode) går ud på at gange ligningerne igennem med passende tal, så koefficienterne til en af de ubekendte bliver ens. Derefter kan den ene ubekendte elimineres ved enten at lægge ligningerne sammen eller trække dem fra hinanden.?

Brugbart svar (0)

Svar #9
06. marts 2021 af mathon

eller
$\small \begin{array}{lllll} \begin{matrix} 5\vec{a}&-&3\vec{b}&=&\vec{x}\\ 2\vec{a}&+&4\vec{b}&=&\vec{y} \end{matrix}\\\\\\ \vec{a}=\frac{\begin{vmatrix} \vec{x} &-3 \\ \vec{y}&4 \end{vmatrix}}{\begin{vmatrix} 5 &-3 \\ 2& 4 \end{vmatrix}}=\frac{4\vec{x}+3\vec{y}}{26}=\frac{1}{26}\cdot \left ( 4\cdot \bigl(\begin{smallmatrix} -18\\\, \, \, \, 20 \end{smallmatrix}\bigr) +3\cdot \bigl(\begin{smallmatrix} -2\\\, \, 34 \end{smallmatrix}\bigr)\right )=\frac{1}{26}\cdot \bigl(\begin{smallmatrix} -78\\182 \end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} -3\\7 \end{smallmatrix}\bigr)\\\\\\ \vec{b}=\frac{\begin{vmatrix} 5 &\vec{x} \\ 2& \vec{y} \end{vmatrix}}{26}=\frac{1}{26}\cdot \left ( 5\cdot \vec{y}-2\cdot \vec{x} \right )=\frac{1}{26}\cdot \left ( 5\cdot \bigl(\begin{smallmatrix} -2\\34 \end{smallmatrix}\bigr) \right )-2\cdot \bigl(\begin{smallmatrix} -18\\20 \end{smallmatrix}\bigr)=\frac{1}{26}\cdot \bigl(\begin{smallmatrix} 26\\130 \end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} 1\\5 \end{smallmatrix}\bigr) \end{array}$

Brugbart svar (0)

Svar #10
07. marts 2021 af mathon

kontrolberegning:

$\small \begin{array}{lllll} 5\overrightarrow{a}-3\overrightarrow{b}=5\cdot \begin{pmatrix} -3\\7 \end{pmatrix}-3\cdot \begin{pmatrix} 1\\5 \end{pmatrix}=\begin{pmatrix} -15\\35 \end{pmatrix}-\begin{pmatrix} 3\\15 \end{pmatrix}=\begin{pmatrix} -18\\20 \end{pmatrix}\\\\\\ 2\cdot \overrightarrow{a}+4\cdot \overrightarrow{b}=2\cdot \begin{pmatrix} -3\\7 \end{pmatrix}+4\cdot \begin{pmatrix} 1\\5 \end{pmatrix}=\begin{pmatrix} -6\\14 \end{pmatrix}+\begin{pmatrix} 4\\20 \end{pmatrix}=\begin{pmatrix} -2\\34 \end{pmatrix} \end{array}$

Skriv et svar til: Vektorer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.