Matematik
Eksponentialfunktion
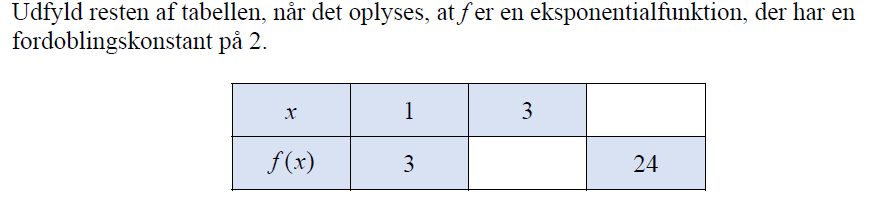
Jeg sidder fast med følgende opgave, jeg kan ikke helt se hvordan jeg skal bestemme de manglende funktionsværdier?
Svar #1
22. oktober 2021 af Anders521
#0 Ved brug af oplysningerne, der er givet i opgaven: 1) f er en eksponentielfunktion: 2) T2 = 2
Bemærk f.eks., at i 1.række haves tallene 1 og 3 og 3 - 1 = 2 ( = T2 ), altså skal der i det hvide felt i 2.række stå 6, fordi tallet 6 er en fordobling af tallet f(1) = 3.
Svar #2
22. oktober 2021 af Albertemads
Det forstår jeg ikke helt? Altså fordoblingskonstanten osv giver mening, men jeg kan ikke forstår hvor du får de 6 fra som resultat?
Svar #3
22. oktober 2021 af Anders521
#2 ...fordi tallet 6 er en fordobling af tallet f(1) = 3. Du ved jo, at produktet af 3·2 gi'r tallet 6.
Svar #4
22. oktober 2021 af Albertemads
Nu giver det mening, skal der så stå 12 i det første hvide felt?
Svar #5
22. oktober 2021 af Anders521
#4 ... Lad os prøve at udvide tabellen: x | 1 | 3 | 5 | 7 | f(x) | 3 | 6 | 12 | 24 |
Svar #9
22. oktober 2021 af Anders521
#5
Tallene 5 og 7 kommer af at have udvidet tabellen såldes at hvert tal 1. række har en afstand på 2. Årsagen til dette skyldes at tallene 1 og 3 har en afstand på i forvejen, og at der oplyses fordoblingskonstanten er 2. Du ved, at fordoblingskonstanten er den x-tilvækst, der fordobler funktionsværdien f(x) til en eksponentielfunktion.
Fordi afstanden mellem tallene 1 og 3 er 2, skal funktionsværdien til 3 være det dobbelte af den foregående funktionsværdi, hvilket kan ses i #8. Her skrives der bl.a. f(3) = 2·f(1). Her er f(1) den foregående funktionsværdi. Da f(1) = 3 ifølge tabellen, så er f(3) = 2·3 = 6. Hvis vi færdiggør tankegangen i #8 har vi flg.
5 + T2 = 7, f(7) = 2·f(5)
Da 2·f(5) = 2· ( 2 ·f(3) ) = 4·6 = 24, f(7) = 24. Altså skal der stå 7 ( og ikke 12) i det tomme felt i 1.række.
Skriv et svar til: Eksponentialfunktion
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.