Matematik

Fourierrække

23. november 2021 af unicorn66 - Niveau: Universitet/Videregående

Bestem summen af Fourierrækken i x = 2p for funktionen f i (1). Svaret er:
a) Summen er ikke konvergent
b) Summen er 2p.
c) Summen er p.

Jeg vil meget gerne have det forklaret i detaljer

Brugbart svar (0)

Svar #1
23. november 2021 af Soeffi

#0. Kender du forskriften for funktionen f?

Svar #2
23. november 2021 af unicorn66

Ja, jeg vedhæfter nu

Vedhæftet fil:67881931-0033-4B12-9F95-5F212B805D66.jpeg

Brugbart svar (0)

Svar #3
23. november 2021 af Soeffi

#0. Indsætter billede:

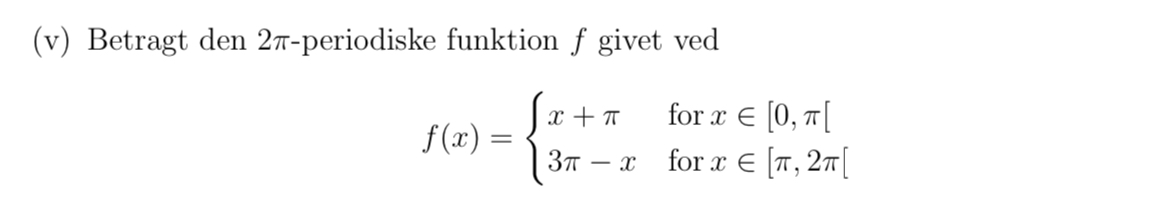
Er p lig med perioden? Har du svaret på evt. foregående spørgsmål i opgaven? Har du Fourier-rækken til funktionen?

Brugbart svar (1)

Svar #4
23. november 2021 af Soeffi

#0. Som jeg forstår opgaven: Find Fourier-rækken (s(x)) for f(x) og vurder om den konvergerer for x = π . Jeg får:...

$s(x)=\frac{3}{2}\pi+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{((-1)^n-1)\cdot cos(nx)}{n^2}$

For x = π...:

$\frac{3}{2}\pi+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{((-1)^n-1)\cdot cos(n\pi)}{n^2}=\frac{3}{2}\pi+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{((-1)^n-1)\cdot (-1)^n}{n^2}=$

$\frac{3}{2}\pi+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{2n}- (-1)^n}{n^2}=\frac{3}{2}\pi+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{1- (-1)^n}{n^2}=$

$\frac{3}{2}\pi+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{1}{n^2}-\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{ (-1)^n}{n^2}=\frac{3}{2}\pi+\frac{2}{\pi}\cdot \frac{\pi^2}{6}-\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{ (-1)^n}{n^2}=$

$\frac{11}{6}\pi-\frac{2}{\pi}\left ( \sum_{n=1}^{\infty}\frac{ 1 }{(2n)^2} -\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2}\right )=\frac{11}{6}\pi-\frac{2}{\pi}\left (\frac{1}{4} \frac{\pi^2}{6} -\frac{-\pi^2}{8}\right )=2\pi$

Brugbart svar (1)

Svar #5
23. november 2021 af Soeffi

#4...rettelse:
$\frac{11}{6}\pi-\frac{2}{\pi}\left ( \sum_{n=1}^{\infty}\frac{ 1 }{(2n)^2} -\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2}\right )=\frac{11}{6}\pi-\frac{2}{\pi}\left (\frac{1}{4} \frac{\pi^2}{6} -{\color{Red} \frac{\pi^2}{8}}\right )=2\pi$

Brugbart svar (1)

Svar #6
25. november 2021 af Soeffi

#4. Note: Man bruger:

$\sum_{n=1}^{\infty}\frac{ 1 }{n^2}=\frac{\pi^2}{6}$

Hvoraf følger:

$\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2}=\frac{\pi^2}{8}$

...idet man deler den første sum i lige og ulige led og får:

$\sum_{n=1}^{\infty}\frac{ 1}{n^2}=\sum_{n=1}^{\infty}\frac{1}{(2n)^2}+\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2} \Leftrightarrow$

$\sum_{n=1}^{\infty}\frac{ 1}{n^2}=\frac{1}{4}\sum_{n=1}^{\infty}\frac{1}{n^2}+\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2} \Leftrightarrow$

$\\\frac{3}{4}\sum_{n=1}^{\infty}\frac{ 1}{n^2}=\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2} \Leftrightarrow$

$\frac{3}{4}\cdot \frac{ \pi^2}{6}=\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2} \Leftrightarrow$

$\sum_{n=1}^{\infty}\frac{ 1}{(2n-1)^2}= \frac{ \pi^2 }{8}$

Skriv et svar til: Fourierrække

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.