Fysik

Bevægelse

17. august 2022 af sabrina132 - Niveau: A-niveau

Hej

Er der nogle der kan hjælpe med opgave c? Filen er vedhæftet.

Vedhæftet fil: Skærmbillede 2022-08-17 kl. 18.42.51.png

Brugbart svar (0)

Svar #1
17. august 2022 af mathon

Svar #2
17. august 2022 af sabrina132

Hej mathon

Jeg kan ikke se dit svar

Brugbart svar (0)

Svar #3
17. august 2022 af mathon

$\small \begin{array}{lllllll} \textbf{c)}\\&&2\cdot a\cdot s=v^2-{v_0}^2\\\\&& v^2={v_0}^2+2\cdot a\cdot s\qquad v>0\\\\&& v(s)=\sqrt{{v_0}^2+2\cdot a\cdot s}\\\\&& v=\sqrt{\left (22.2222\;\mathrm{\frac{m}{s}} \right )^2+2\cdot \left ( -2\;\mathrm{\frac{m}{s^2}} \right )\cdot s}\\\\&& v=\sqrt{\left (22.2222\;\mathrm{\frac{m}{s}} \right )^2- \left ( 4\;\mathrm{\frac{m}{s^2}} \right )\cdot s} \quad \textup{hvis graf kan indtegnes}\end{array}$

Svar #4
17. august 2022 af sabrina132

hej mathon

Hvordan er du nået til tredje punkt. Altså hvordan laver du den om til en funktion?

Svar #5
17. august 2022 af sabrina132

Og hvordan forsvinder v^2 og der istedet står v(s)

Svar #6
17. august 2022 af sabrina132

Og hvordan kan det tegnes ind på TI-inspire?

Brugbart svar (0)

Svar #7
17. august 2022 af ringstedLC

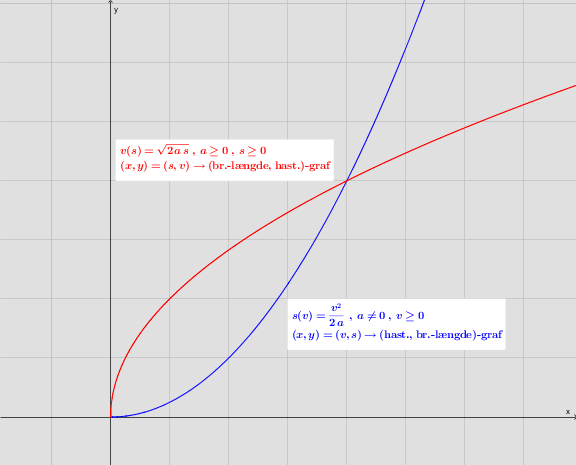
Funktionen i c) giver desværre en (br.-længde, hast.)-graf og ikke en (hast., br.-længde), hvor hastigheden v er den uafh.- variabel og s(v) er den afh. variabel.

Brugbart svar (0)

Svar #8
17. august 2022 af ringstedLC

#4 og #5:

$\begin{align*} v^2 &= {v_0}^2+2\cdot g\cdot s\;,\;v>0 \\ v &= \sqrt{\underset{\textup{konst.}}{\underbrace{{v_0}^2 +2\cdot g}}\;\;\cdot \!\underset{\textup{uafh.\,var.}}{\underbrace{s}}} \\ \underset{\textup{afh.\,var.}}{\underbrace{v(s)}} &= \sqrt{{v_0}^2+2\cdot g\cdot s} \end{align*}$

#6: Definér og plot den rigtige funktion.

Svar #9
17. august 2022 af sabrina132

Hvordan kan det så være, at min fysiklærer har skrevet (hast, bremselængde)-graf?

Svar #10
17. august 2022 af sabrina132

Kan det passe, at det skal se sådan ud?

Vedhæftet fil:Skærmbillede 2022-08-17 kl. 21.21.10.png

Brugbart svar (0)

Svar #11
17. august 2022 af ringstedLC

#9: Dét bestemmer han jo. c) i #3 er ikke den rigtige funktion for den ønskede graf.

Brug den første linje i #3 og isolér bremselængden s. Lav så en bremselængdefunktion af hast. v.

#10: Nej, det er jo en konstant.

$\begin{align*} f1(x) &= \sqrt{{v_0}^2+2\cdot 9.82\cdot {\color{Red} x}} \\ v_0 &= 80\,\textup{km/h}=\tfrac{80}{3.6}\,\textup{m/s}\;{\color{Red} \neq }\;3\,\textup{m/s} \end{align*}$

Brugbart svar (0)

Svar #12
18. august 2022 af mathon

$\small \small \begin{array}{llllll} \textup{bremsearbejde}=\textup{kinetisk energi\ae ndring}\\\\ \textbf{konstant bremsekraft}\\\\ F_{\textup{brems}}\cdot L_{\textup{brems}}=\frac{1}{2}\cdot m\cdot v^2-0\\\\ m\cdot a_{\textup{brems}}\cdot L_{\textup{brems}}= \frac{1}{2}\cdot m\cdot v^2\\\\ a_{\textup{brems}}\cdot L_{\textup{brems}}= \frac{1}{2}\cdot v^2\\\\\\\qquad L_{\textup{brems}}=\frac{v^2}{2\cdot a_{\textup{brems}}} \end{array}$

Brugbart svar (0)

Svar #13
18. august 2022 af mathon

eller noteret

$\small \small \begin{array}{llllll} \textup{bremsearbejde}=\textup{kinetisk energi\ae ndring}\\\\ \textbf{konstant bremsekraft}\\\\ F_{\textup{brems}}\cdot L_{\textup{brems}}=\frac{1}{2}\cdot m\cdot v^2-0\\\\ m\cdot\underset{\textbf{konstant}}{\underbrace{ a_{\textup{brems}}}}\cdot L_{\textup{brems}}= \frac{1}{2}\cdot m\cdot v^2\\\\ a_{\textup{brems}}\cdot L_{\textup{brems}}= \frac{1}{2}\cdot v^2\\\\\qquad L_{\textup{brems}}=\left (\frac{1}{2\cdot a_{\textup{brems}}} \right )\cdot v^2\\\\\\ \qquad\mathbf{ L_{\textup{brems}}=k\cdot v^2} \end{array}$

Svar #14
18. august 2022 af sabrina132

#11

Ser grafen rigtig ud?

Svar #15
18. august 2022 af sabrina132

#11

Ser grafen rigtig ud?

#11

Mener du en s(t)-graf

Vedhæftet fil:Skærmbillede 2022-08-18 kl. 17.33.57.png

Brugbart svar (0)

Svar #16
20. august 2022 af ringstedLC

#8 rettelse
#4 og #5:

$\begin{align*} v^2 &= {v_0}^2+2\cdot {\color{Red} a}\cdot s\;,\;v>0 \\ v &= \sqrt{\underset{\textup{konst.}}{\underbrace{{v_0}^2 +2\cdot {\color{Red} a}}}\;\;\cdot \!\underset{\textup{uafh.\,var.}}{\underbrace{s}}} \\ \underset{\textup{afh.\,var.}}{\underbrace{v(s)}} &= \sqrt{{v_0}^2+2\cdot {\color{Red} a}\cdot s} \end{align*}$

#6: Definér og plot den rigtige funktion.

Brugbart svar (0)

Svar #17
20. august 2022 af ringstedLC

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #18
20. august 2022 af ringstedLC

Den blå graf kan anvendes til at tilpasse sin afstand* til den forankørende m.m.

* Afstand_min. ≈ standselængde = br.-længde + reaktionlængde.

Den røde graf kan bruges til at anslå begyndelseshastigheden af en katastrofeopbremsning ved at måle et eventuelt bremsespors længde. Det bruges fx ved trafikulykker.

Den kan ligeledes bruges til fastlæggelse af hastighedsbegrænsninger.

Svar #19
20. august 2022 af sabrina132

hvilket tal, skal jeg indsætte som accelerationen?

Brugbart svar (0)

Svar #20
20. august 2022 af ringstedLC

Genlæs opgaveteksten om antagelser, tegn grafen med a som en skyder og se effekten af at ændre værdien.

Skriv et svar til: Bevægelse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.