Matematik

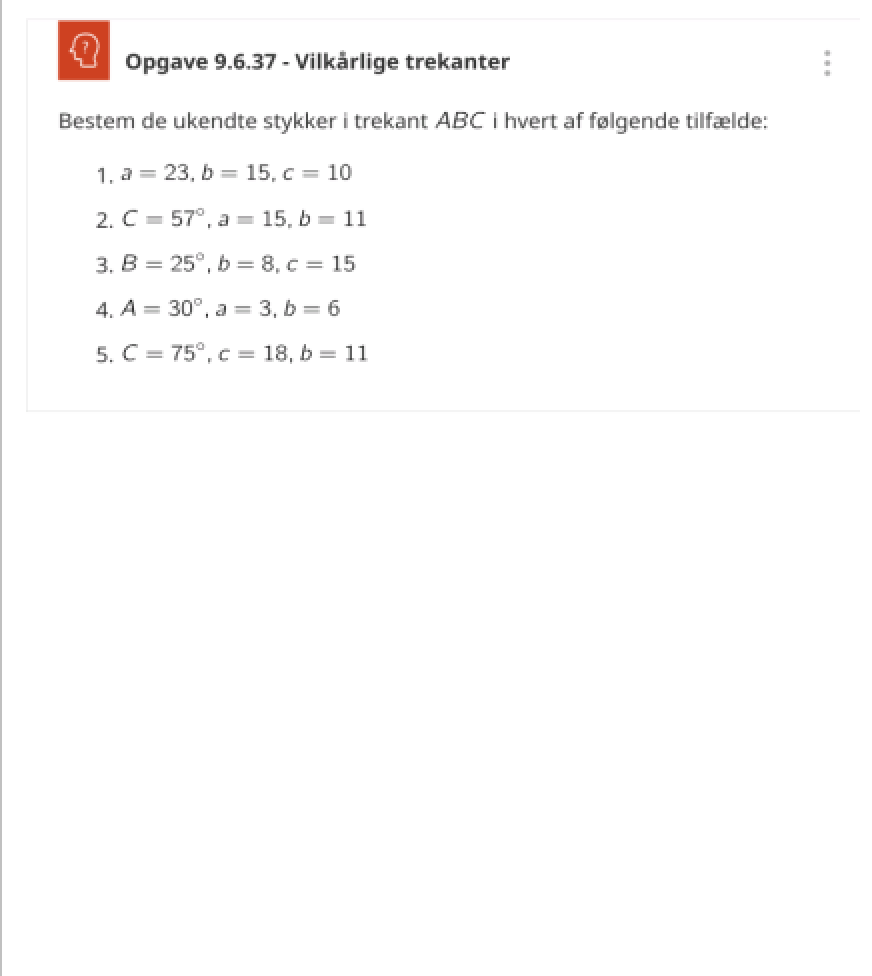
vilkårlig trekanter

24. september 2022 af ho123 - Niveau: B-niveau

forstå ikke hvordan man skal bruge Cosinusrelationerne

Vedhæftet fil: Skærmbillede 2022-09-24 kl. 14.12.31.png

Brugbart svar (0)

Svar #1
24. september 2022 af peter lind

Hvad har du af problemer med de opgaver? Du kan jo bare skrive formlen op med de kendte værdier indsat

Svar #2
24. september 2022 af ho123

for eksempel med opg 2 så jeg bergner dem så for jeg ikke det svar jeg skal have

Brugbart svar (0)

Svar #3
24. september 2022 af mathon

$\begin{array}{llllll} \textbf{2)}\\&&c^2=a^2+b^2-2\cdot a\cdot b\cdot \cos(C)\\\\&& c=\sqrt{15^2+11^2-\cdot 2\cdot 15\cdot 11\cdot \cos(57\degree)}\quad \textup{vinkelm\aa let i }grader \end{array}$

Brugbart svar (0)

Svar #4
25. september 2022 af mathon

$\small \begin{array}{llllll} \textbf{2)}\\&&c^2=a^2+b^2-2\cdot a\cdot b\cdot \cos(C)\\\\&& c=\sqrt{15^2+11^2- 2\cdot 15\cdot 11\cdot \cos(57\degree)}=12.9\\\\\\&& \cos(A)=\frac{b^2+c^2-a^2}{2\cdot b\cdot c}=\frac{15^2+12.9^2-15^2}{2\cdot 11\cdot 12.9}=0.219908\\\\&& A=\cos^{-1}\left (0.219908 \right )=77.3\degree \end{array}$

Brugbart svar (0)

Svar #5
25. september 2022 af ringstedLC

Brugbart svar (0)

Svar #6
25. september 2022 af ringstedLC

#0: En typisk fejl er, at man ikke får relateret den rigtige vinkel til den tilhørende side eller omvendt. Husk at lille "bogstav" (en side) er modstående (rører ikke) til vinklen med det samme store "bogstav". Vinkel A har altså vinkelbenene b og c.

Se mere på https://www.webmatematik.dk/lektioner/matematik-b/trigonometri/cosinusrelationerne

Brugbart svar (0)

Svar #7
25. september 2022 af mathon

$\small \small \begin{array}{llllll} \textbf{3)}\\&&8^2=15^2+a^2-2\cdot 15\cdot a\cdot \cos(25\degree)\\\\&& 64=225+a^2-30\cdot \cos(25\degree)\cdot a\\\\&& a^2-30\cdot \cos(25\degree)\cdot a+161=0\\\\&&a=\left\{\begin{matrix} 8.7147\\ 18.4745 \end{matrix}\right.\\\\&&A=\left\{\begin{matrix} \cos^{-1}\left ( \frac{8^2+15^2-8.7147^2}{2\cdot 8\cdot 15} \right )\\ \cos^{-1}\left ( \frac{8^2+15^2-18.4745^2}{2\cdot 8\cdot 15} \right ) \end{matrix}\right.\\\\&& C=\left\{\begin{matrix} 180\degree-\left (25\degree +A_1 \right )\\ 180\degree-\left (25\degree+A_2 \right ) \end{matrix}\right. \end{array}$

Brugbart svar (0)

Svar #8
28. september 2022 af mathon

$\small \small \begin{array}{llllll} \textbf{4)}\\&&3^2=6^2+c^2-2\cdot 6\cdot c\cdot \cos(30\degree)\\\\&& 9=36+c^2-12\cdot \frac{\sqrt{3}}{2}\cdot c\\\\&& c^2-6\sqrt{3}\cdot c+27=0\\\\&& \left (c- 3\sqrt{3} \right )^2=0\\\\&& c=3\sqrt{3}\\\\&\textup{Da }&\textup{siden }a \textup{ og }h_c\textup{ er sammenfaldende er }\\\\&&B=90\degree\\\\ &&C=90\degree-30\degree=60\degree \end{array}$

Brugbart svar (0)

Svar #9
28. september 2022 af mathon

$\small \small \begin{array}{llllll} \textbf{5)}\\&&18^2=11^2+a^2-2\cdot 11\cdot a\cdot \cos(75\degree)\\\\&& 324=121+a^2-22\cdot \cos\left ( 75\degree \right )\cdot a\\\\&& a^2-22\cdot \cos\left ( 75\degree \right )\cdot a-203=0,\quad a>0\\\\&& \\\\&& a=17.3765\approx 17.38\\\\\\&& \cos\left ( A \right )=\frac{b^2+c^2-a^2}{2\cdot b\cdot c}=\frac{11^2+18^2-17.3765^2}{2\cdot 11\cdot 18}=0.361258\\\\&& A=\cos^{-1}\left (0.361258 \right )=68.82\degree \\\\\\&&\cos(B)=\frac{a^2+c^2-b^2}{2\cdot a\cdot c}=\frac{17.3765^2+18^2-11^2}{2\cdot 17.3765\cdot 18}=0.807193\\\\&&B=\cos^{-1}\left (0.807193 \right )=36.18\degree\\\\&&\\\\\\&\textup{vinkelkontrol:}\\&&A+B+C=68.82\degree+36.18\degree+75\degree=180\degree \end{array}$

Skriv et svar til: vilkårlig trekanter

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.