Matematik

Arealbestemmelse

19. maj 2023 af Curiosity4life - Niveau: B-niveau

Hej, jeg ved ikke hvordan den her opgave skal gribes an:

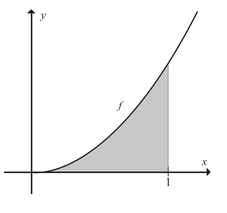
En funktion f er givet ved forskriften f(x)=a*x^2

Det grå område afgrænses af grafen for f, x-aksen og linjen med ligningen x=1

Bestem tallet a så arealet af det grå område er 2

Tusind tak på forhånd!

Brugbart svar (0)

Svar #1
19. maj 2023 af MentorMath

Hej, har du mulighed for at vise et billede af det grå område?

Svar #2
19. maj 2023 af Curiosity4life

Her er det:

Vedhæftet fil:Skærmbillede 2023-05-19 kl. 14.15.33.png

Brugbart svar (0)

Svar #3
19. maj 2023 af mathon

Brugbart svar (1)

Svar #4
19. maj 2023 af mathon

$\begin{array}{lllll} \int_{0}^{1}ax^2\;\mathrm{d}x=\left [\frac{a}{3} x^3 \right ]_0^1=\frac{a}{3}\cdot \left ( 1^3-0^3 \right )=\frac{a}{3}\cdot 1=\frac{1}{3}a\\\\\\ \frac{1}{3}a=2\\\\ a=2\cdot 3=6 \end{array}$

Svar #5
19. maj 2023 af Curiosity4life

#4
$\begin{array}{lllll} \int_{0}^{1}ax^2\;\mathrm{d}x=\left [\frac{a}{3} x^3 \right ]_0^1=\frac{a}{3}\cdot \left ( 1^3-0^3 \right )=\frac{a}{3}\cdot 1=\frac{1}{3}a \end{array}$

Ahhhh, det havde jeg også gjort, men da jeg tjekkede efter fik jeg ikke 2 som arealet. Men kan godt se, at jeg nok havde kommet til at efterregne det forkert, da det nu går op. Tusind tak!

Brugbart svar (0)

Svar #6
19. maj 2023 af ringstedLC

Kontrol:

$\begin{align*} A &= \left |\int_{0}^{1}\!f_2(x)\,\mathrm{d}x \right | \\ &= \left | F_2(1)-F_2(0) \right | \\ A &= \left | \tfrac{6}{3}\cdot 1^3-0 \right |=2 \end{align*}$

Svar #7
19. maj 2023 af Curiosity4life

#6
Kontrol:

$\begin{align*} A &= \left |\int_{0}^{1}\!f_2(x)\,\mathrm{d}x \right | \\ &= \left | F_2(1)-F_2(0) \right | \\ A &= \left | \tfrac{6}{3}\cdot 1^3-0 \right |=2 \end{align*}$

Ja det har jeg også fået, men tak!

Skriv et svar til: Arealbestemmelse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.