Matematik

Bestem tallet k og bestem radius i den store cirkel med 3 decimaler

10. marts kl. 17:51 af TaterTot8514 - Niveau: B-niveau

Godaften allesammen.

Jeg sidder lidt fast i to af opgaverne i den nye aflevering jeg har fået.

Det drejer sig om opgave 6, hvor vi ved at funktionen f er givet ved f(x)=k*√x, hvor k er et tal. Derudover får vi oplyst, at f(4)=26. I denne opgave skal jeg bestemme tallet k, og da det ikke er noget vi har gjort førhen, så føler jeg mig lost i opgaven.

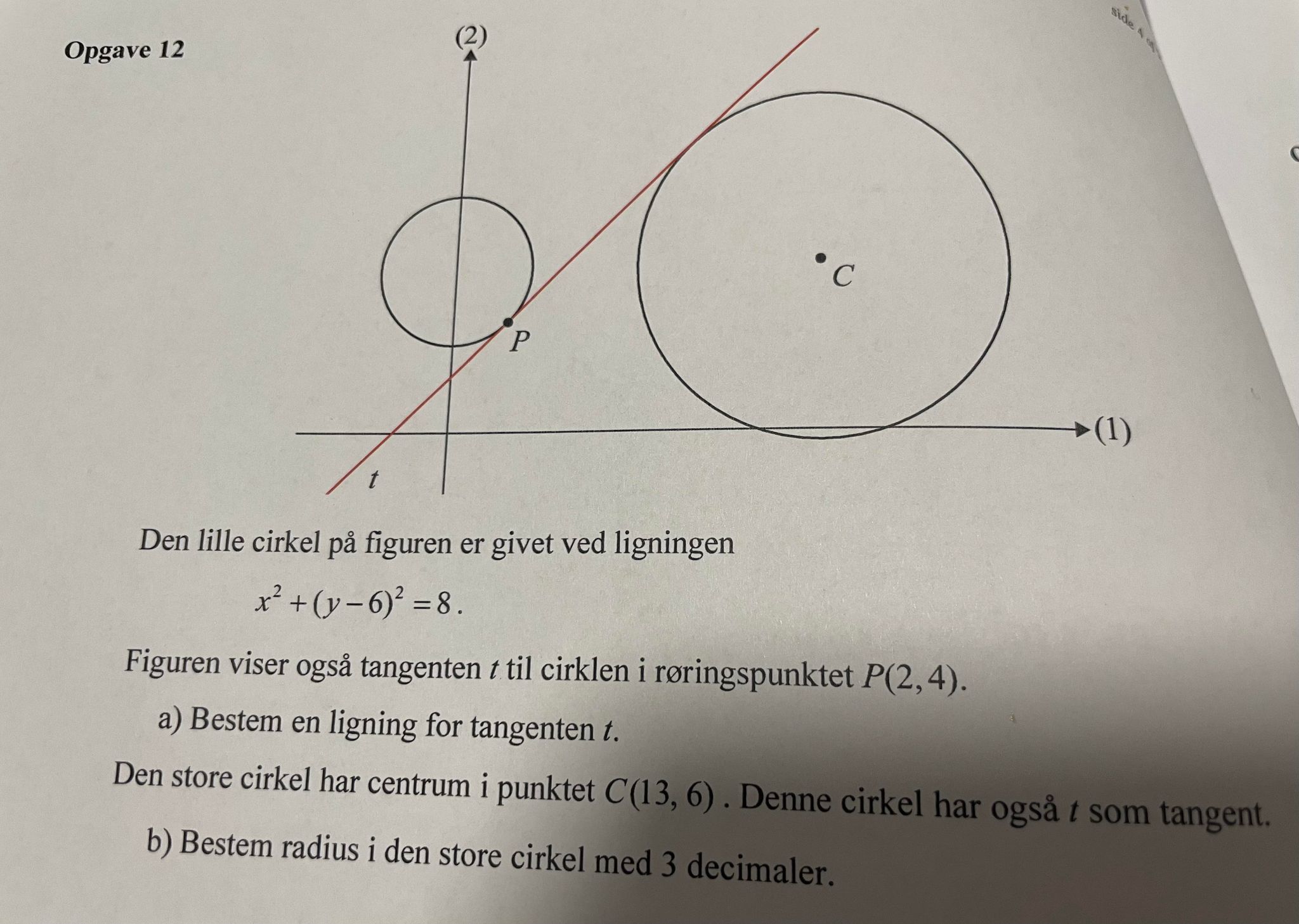
Derudover har jeg opgave 12, hvor jeg skal bestemme radius i den store cirkel med 3 decimaler. Denne cirkel har centrum i punktet (13, 6) og har også t som tangent. Jeg har fundet frem til at radius er 40 el. 6,325^2 - dog har jeg fundet det via Nspire, men jeg skal vise udregningen og den del sidder jeg fast i.

På forhånd mange tak for hjælpen! :)

Vedhæftet fil: 431850790_938971604292936_1838691056559031682_n.jpg

Brugbart svar (1)

Svar #1
10. marts kl. 18:10 af ringstedLC

Opg. 6

$\begin{align*} f(x) &= k\cdot \sqrt{x} &&,\;k\in\mathbb{R} \\ f(4)=26 &= k\cdot \sqrt{4} \Rightarrow k=\frac{26}{\sqrt{4}}=... \end{align*}$

Brugbart svar (0)

Svar #2
10. marts kl. 18:11 af ringstedLC

Svar #3
10. marts kl. 18:17 af TaterTot8514

#1
Opg. 6

$\begin{align*} f(x) &= k\cdot \sqrt{x} &&,\;k\in\mathbb{R} \\ f(4)=26 &= k\cdot \sqrt{4} \Rightarrow k=\frac{26}{\sqrt{4}}=... \end{align*}$

Nu giver det lidt mere mening, jeg havde nemlig også prøvet at sidde og regne lidt forskelligt, men jeg fandt altid frem til nogle underlige tal, men nu hvor jeg kan se, hvor tallene skal placeres så giver det egentlig mening!
Når jeg så regner det sidste ud, så får jeg k til at blive 13, er det rigtigt?

Brugbart svar (0)

Svar #4
10. marts kl. 18:41 af ringstedLC

Opg. 12

$\begin{align*} \textup{Tangent}:x-y+2 &= 0 \end{align*}$

$\begin{align*} \textup{dist}\bigl(C,t) &= \frac{\left | a\,x_1+b\,y_1+c \right |}{\sqrt{a^2+b^2}} &&\textup{formel (74)} \\ &= \frac{\left | 13-6+2 \right |}{\sqrt{2}}=6.3639...=6.364 \end{align*}$

Radius er nok snarere √40.5

Brugbart svar (1)

Svar #5
10. marts kl. 18:43 af ringstedLC

#3 Tegn grafen og se om (4, 26) ligger på den.

Svar #6
10. marts kl. 19:23 af TaterTot8514

#4
Opg. 12

a)

$\begin{align*} \textup{Tangent}:x-y+2 &= 0 \end{align*}$

b)

$\begin{align*} \textup{dist}\bigl(C,t) &= \frac{\left | a\,x_1+b\,y_1+c \right |}{\sqrt{a^2+b^2}} &&\textup{formel (74)} \\ &= \frac{\left | 13-6+2 \right |}{\sqrt{2}}=6.3639...=6.364 \end{align*}$

Radius er nok snarere √40.5

Jeg kan ikke helt finde ud af hvilken formel du bruger i a) , jeg har nemlig brugt a=((y2-y1)/(x2-x1)), og fra det får jeg -1, hvor jeg så bruger formlen a*c = -1, og får a_t=1.

Nu bruger jeg så formeln y=a_t*(x-x₁)+y_{1, og jeg finder frem til at y=x+2}

Svar #7
10. marts kl. 19:24 af TaterTot8514

#5
#3 Tegn grafen og se om (4, 26) ligger på den.

Det gjorde den! Tusind tak for hjælpen :)

Brugbart svar (1)

Svar #8
10. marts kl. 20:20 af ringstedLC

#6 Der er to distanceformler som bruges afhængigt af linjens ligningsform:

$\begin{align*} a\cdot (x-x_1)+b\cdot (y-y_0) &= 0\;,\;\vec{n}=\binom{a}{b} &&&\textup{formel (71)} \\ \overrightarrow{C_1P}=\binom{2-0}{4-6} &= \binom{2}{-2} \\ t:2\cdot (x-2)-2\cdot (y-4) &= 0 \\ x-2-y+4 &= 0 \\ x-y+2 &= 0 \Rightarrow & y &= x+2 \\ &&\textup{dist}\bigl(C,t) &= \frac{\left | a\,x_1+b-y_1 \right |}{\sqrt{a^2+1}} &\textup{formel ({\color{Red} 73})} \\ &&&= \frac{\left | 13+2-6 \right |}{\sqrt{2}} \\ &&\textup{dist}\bigl(C,t) &= 6.364 \end{align*}$

Svar #9
10. marts kl. 20:56 af TaterTot8514

#8
#6 Der er to distanceformler som bruges afhængigt af linjens ligningsform:

$\begin{align*} a\cdot (x-x_1)+b\cdot (y-y_0) &= 0\;,\;\vec{n}=\binom{a}{b} &&&\textup{formel (71)} \\ \overrightarrow{C_1P}=\binom{2-0}{4-6} &= \binom{2}{-2} \\ t:2\cdot (x-2)-2\cdot (y-4) &= 0 \\ x-2-y+4 &= 0 \\ x-y+2 &= 0 \Rightarrow & y &= x+2 \\ &&\textup{dist}\bigl(C,t) &= \frac{\left | a\,x_1+b-y_1 \right |}{\sqrt{a^2+1}} &\textup{formel ({\color{Red} 73})} \\ &&&= \frac{\left | 13+2-6 \right |}{\sqrt{2}} \\ &&\textup{dist}\bigl(C,t) &= 6.364 \end{align*}$

Okay, nu giver det mening! Det er fordi vi har brugt andre formler på HF! Dog giver det mening og jeg finder frem til samme resultat.

Mange tak for hjælpen til opgaverne! :)

Skriv et svar til: Bestem tallet k og bestem radius i den store cirkel med 3 decimaler

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.