Forvirring mht. bevis af ekstremalværdisætningen

Det drejer sig om beviset som føres ved brug af ruselemmaet: kort sagt, så sættes M til at være lig supremum af funktionsværdierne for alle x i et afsluttet og begrænset interval [a,b]. Så halveres intervallet, og vi arbejder videre med det interval, som M igen har supremum over. Og så videre. Vi benytter her at .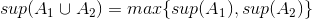

Ruserne bestemmer et tal, og dette er netop det punkt c  som afbildes over i M via f(c), altså supremum/maksmimum. Dette viser vi ved at vise at f(c) er større end eller lig M (den omvendteu lighed er oplagt). Vi bruger kontinuitet, så vi ved at når x er inden for delta af c, så gælder at 

.

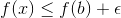Her kommer så det jeg ikke forstår. Vi gør intervallerne mindre , sådan at vi til sidst står med et interval med længde som er mindre end delta, og så er alle x i dette interval selvfølgelig inden for delta af c (som også ligger i intervallet, da dette jo er det tal vi "fanger"). Så står der at

Hvorfor er M mindre end eller lig supremum af f(x) for alle x i [a,b] (det oprindelige interval)? Er dette ikke netop hvad M er?