Matematik
Vektorer, trekantsberegning?
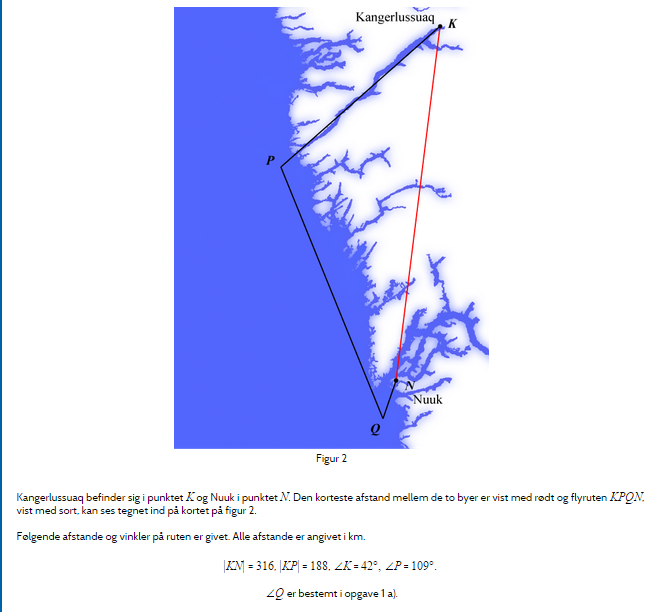
Hej - Jeg sidder her med en undren omkring hvilke muligheder jeg kan benytte mig af, for at finde den samlede længde for flyruten KPQN. (se vedhæftede billede). Er jeg ude i noget mulig vektorregning? (dog forstår jeg så ikke hvordan uden to givne koordinater), eller er jeg ovre i trekantsopdeling med udelukkelse af et punkt?
Svar #1
14. april 2015 af Heptan
Ved du noget om punkt Q, udover dens vinkel, og at det ligger syd for Nuuk? :P
Svar #2
14. april 2015 af Heptan
Opgaven kan løses udelukkende ved at dele den op i to trekanter, fx trekant PKN og PNQ. Du kan så prøve at finde ud af alt der er værd at vide om disse trekanter.
Da vinkelsummen i en firkant er 360º, kan vinkel N beregnes.
Da du kender to sider og en vinkel i trekant PKN kan du beregne de resterende vinkler ved hjælp af cosinusrelationerne og sinusrelationerne.
Vinkel QNP er lig med vinkel QNK minus vinkel PNK. Vinkel QPN kan beregnes ved hjælp af vinkelsummen i trekant PNQ. Nu kan sidelængderne |PQ| og |QN| endelig beregnes vha. sinusrelationerne i trekant PNQ.
Svar #3
15. april 2015 af Mariostar (Slettet)
Mange tak for svaret, det er brugbart - og nej, jeg ved intet andet om punkt Q ;-)
Endvidere...giver det mening hvis selve vinkelsummen for trekant PKN giver over 180?
På baggrund af dette spørgsmål, så forstås der at, jeg har regnet mig til følgende med fed:
|PN| = 216.57 vinkel K = 42
|KP| = 188 vinkel N = 17.8
|KN| = 316 vinkel P = 163.6
Svar #4
15. april 2015 af Andersen11 (Slettet)
#3
Det anføres i det vedlagte, at vinkel Q er bestemt i et tidligere spm. Hvad er denne vinkel bestemt til?
I trekant PKN kender man de to sider PK og KN og den mellemliggenden vinkel K, og man kan da bestemme |PN| ved at benytte en cosinusrelation, og din bestemmelse er korrekt. Man kan da bestemme vinkel KPN i trekant PKN ved at benytte en anden cosinusrelation i trekant PKN, og man finder
vPKN = 102,489º.
Herefter beregnes vinkel vQPN = 109º - 102,489º = 6,511º
Hvis vinkel Q er kendt, kender man nu i trekant PQN de to vinkler Q og vQPN, og dermed alle tre vinkler, og man kender siden PN, og man kan derfor beregne |QN| ved at benytte sinusrelationerne i trekant PQN.
Svar #5
16. april 2015 af Mariostar (Slettet)
vQ er 39.1º
Jeg har nu siddet og regnet, og jeg er kommet til en masse resultater, som jeg vil sige giver super mening.
-Andersen og Heptan, i skal have mange tak :-)
Jeg får nu:
|KP| = 188 km
|PQ| = 184.955 km
|QN| = 38.9388 km
Svar #6
17. april 2015 af Andersen11 (Slettet)
#5
Jeg finder |PQ| = 245,391 km . Du har benyttet sin(39,1º-6,511º) i stedet for sin(39,1º+6,511º) .
Svar #7
17. april 2015 af bonnie95 (Slettet)
Jeg forstår ikke helt hvordan i kommer frem til med trekanten PNQs resultater:-)
Svar #8
17. april 2015 af Andersen11 (Slettet)
#7
I trekant PNQ kender man til sidst
|PN| = 216,57
Q = 39,1º (ifølge din egen oplysning)
vQPN = 109º - 102,489º = 6,511º .
Derfor har man af sinusrelationerne
|QN|/sin(vQPN) = |PN|/sin(Q) = |PQ|/sin(vPNQ} = |PQ|/sin(Q+vQPN)
hvorfor
|QN| = |PN|·sin(vQPN)/sin(Q) = 216,57·sin(6,511º)/sin(39,1º) = 38,94 km
og
|PQ| = |PN|·sin(Q+vQPN)/sin(Q) = 216,57·sin(45,611º)/sin(39,1º) = 245,39 km
Svar #9
18. april 2015 af Whut (Slettet)
#8
Hvorfor er vPNQ = Q+vQPN? Skulle det ikke være vPNQ = 180 - (Q+vQPN)?
Svar #10
18. april 2015 af Andersen11 (Slettet)
#9
De er da heller ikke lig med hinanden, og det er heller ikke påstået nogetsteds ovenfor. De to vinkler er, som du selv angiver, supplementvinkler, og derfor har de samme sinus, som det er angivet i #8.
Beregningerne i #8 er korrekte.
Svar #11
18. april 2015 af Whut (Slettet)
#10
OK. Jeg avendte vinklerne til at måle i radianer, hvilket forvirrede mig indtil jeg ændrede det til grader. Du har helt ret. Tak for hjælpen.
Skriv et svar til: Vektorer, trekantsberegning?
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.