Matematik
Halveringstid og eksponentialfunktion
Hej!
Jeg sidder med en opgave i matematik som jeg ikke kan finde en løsning på.
Så langt her er jeg nået (men er ikke sikker på at det er rigtigt på nogen måde):
T1/2 = log(a) / log(1/2)
5730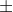 40 = log(a) / log(1/2)
40 = log(a) / log(1/2)
Jeg vil finde a, så log(a) isoleres:
log(a)= 5730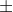 40 * log(1/2)
40 * log(1/2)
Jeg vil gerne lave en eksponentialfunktion (f(x)=b*ax)
Jeg håber på en finde en måde at fjerne log, så jeg blot har a tilbage... Ved ikke om dette er den rigtige start, men håber I vil hjælpe mig:-)
Herunder ses opgaven (hvis det gør det nemmere):
Kulstof 14 er navnet på en metode til at datere (tidsbestemme) organisk materiale. Ideen er at organismen mens den er levende løbende via stofskiftet erstatter C-atomer i kroppen så der derved hele tiden er samme fordeling af isotoper som gennemsnitligt på jorden. Når organismen dør vil denne udskiftning stoppe og radioaktivt henfald af ustabile isotoper vil derfor ændre på sammensætningen af isotoper uden at denne hele tiden ”nulstilles”. Radioaktive henfald kan beskrives ved en eksponentielt aftagende funktion og man kan derved regne ud hvor længe siden dødt organisk materiale har været dødt hvis man måler forholdet mellem den stabile isotop (_^12)C og den radioaktive isotop (_^14)C. Halveringstiden for (_^14)C er 5730 ± 40 år
Opgave 1:
Opstil en model der viser andelen af oprindeligt (_^14)C som funktion af år efter organismens død både for laveste-, højeste- og gennemsnitshalveringstid.
Svar #2
04. oktober 2016 af dittemy1 (Slettet)
Tak for svaret!
Hvordan beregner man så dette: a=105730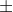 40*log(1/2) ?
40*log(1/2) ?
Svar #3
04. oktober 2016 af peter lind
Det slår du op på din lommeregner. Ser lige at din udregning er forkert t½ =ln(½)/ln(a)
Skriv et svar til: Halveringstid og eksponentialfunktion
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






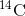 i forhold til totalmængden af
i forhold til totalmængden af 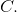
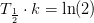 hvor
hvor 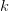 er henfaldskonstanten
er henfaldskonstanten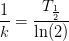
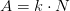
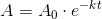 aktiviteten måles i antal henfald pr gram pr. minut
aktiviteten måles i antal henfald pr gram pr. minut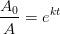
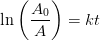
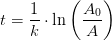
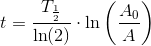
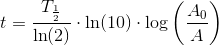
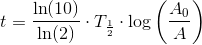
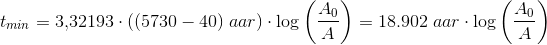
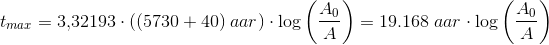
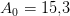 henfald pr minut pr. gram total mængde carbon.
henfald pr minut pr. gram total mængde carbon.