Differentialregning: bevis for (f(x)+g(x))'=f'(x)+g'(x)

10. juni 2017 af 97an (Slettet) - Niveau: B-niveau

Hej. Kan i hjælpe med dette: Lav et bevis for regnlereglen (f(x)+g(x))'=f'(x)+g'(x)

Brugbart svar (0)

Svar #1
10. juni 2017 af sjls

Prøv at sætte 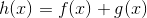h(x)=f(x)+g(x) . Så er 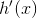h'(x) defineret som:

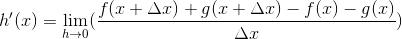
$h'(x)=\lim_{h\rightarrow 0}(\frac{f(x+\Delta x)+g(x+\Delta x)-f(x)-g(x)}{\Delta x})$

hvilket kan omskrives til

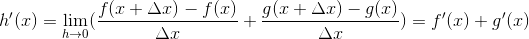
$h'(x)=\lim_{h\rightarrow 0}(\frac{f(x+\Delta x)-f(x)}{\Delta x}+\frac{g(x+\Delta x)-g(x)}{\Delta x})=f'(x)+g'(x)$

Dermed er 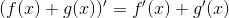(f(x)+g(x))'=f'(x)+g'(x)

Forstår du?

Svar #2
11. juni 2017 af 97an (Slettet)

Jaaa tusind tak!

Skriv et svar til: Differentialregning: bevis for (f(x)+g(x))'=f'(x)+g'(x)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.