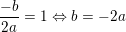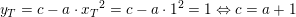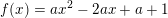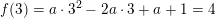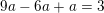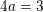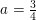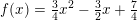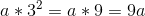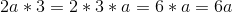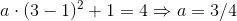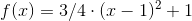Matematik

Find polynomiums forskrift ud fra toppunkt og hvor den går gennem

15. juli 2017 af lottehvorerduhenne (Slettet) - Niveau: B-niveau

Hej alle.

Jeg sidder med en rigtig dum opgave, og jeg kunne virkelig godt bruge hjælp til denne:

Et andengradspolynomium f har toppunkt (1,1) og går gennem (3,4). Find polynomiets forskrift.

Jeg ville umidelbart bruge y=ax^2+bx+c, men jeg aner ikke hvordan.

Tak på forhånd!

Brugbart svar (0)

Svar #1
15. juli 2017 af JulieW99

Er det med eller uden hjælpemidler?

- - -

Vh Julie

Svar #2
15. juli 2017 af lottehvorerduhenne (Slettet)

Det er med. Jeg har i hvert fald ikke fået besked på andet. :-)

Vh. Freja

Brugbart svar (0)

Svar #3
15. juli 2017 af JulieW99

Jeg vender lige tilbage om en halv times tid ca. :)

- - -

Vh Julie

Svar #4
15. juli 2017 af lottehvorerduhenne (Slettet)

Tusinde tak!

Brugbart svar (0)

Svar #5
15. juli 2017 af Soeffi

#0 Et andengradspolynomium f har toppunkt (1,1) og går gennem (3,4) .

Der gælder:

1) f(x) = ax² + bx + c

2) f(1) = 1 og f´(1) = 0

3) 4 = a·3² + b·3 + c

Brugbart svar (0)

Svar #6
15. juli 2017 af JulieW99

Okay, jeg kunne kun løse det så værdien for a var korrekt

- - -

Vh Julie

Brugbart svar (0)

Svar #7
15. juli 2017 af mathon

eller
$\small \frac{-b}{2a}=1\Leftrightarrow b=-2a$

                 $\small y_T=c-a\cdot {x_T}^2=c-a\cdot 1^2=1\Leftrightarrow c=a+1$
hvoraf:
                $\small f(x)=ax^2-2ax+a+1$
og
                 $\small f(3)=a\cdot 3^2-2a\cdot 3+a+1=4$

$\small 9a-6a+a=3$

$\small 4a=3$

$\small a=\tfrac{3}{4}$

$\small \small f(x)=\tfrac{3}{4}x^2-\tfrac{3}{2}x+\tfrac{7}{4}$

Svar #8
15. juli 2017 af lottehvorerduhenne (Slettet)

Hvad er det du har gjort på anden linje? Det er jeg ikke helt sikker på at jeg forstår.

Svar #9
15. juli 2017 af lottehvorerduhenne (Slettet)

Hvordan er du kommet frem til 9a - 6a? :-)

Brugbart svar (1)

Svar #10
15. juli 2017 af Mathias7878

a * 3^2 = a * 9 = 9a

2a*3 = 2*3*a = 6*a = 6a

- - -

Svar #11
15. juli 2017 af lottehvorerduhenne (Slettet)

Aaah, makes sense!

Men jeg er stadig ikke sikker på at jeg forstår anden linje. :-/

Brugbart svar (0)

Svar #12
15. juli 2017 af Mathias7878

Anden linje som er 9a - 6a + a = 3?

- - -

Svar #13
15. juli 2017 af lottehvorerduhenne (Slettet)

Nej. Den som er yT = c - a *yT^2 = c - a * 1^2 = 1 <=> c = a + 1. :-D

Svar #14
15. juli 2017 af lottehvorerduhenne (Slettet)

Faktisk forstår jeg slet ikke hvordan det hele er regnet ud.

Jeg har prøvet at sætte det ind i Geogebra, fordi vi skal angive punkterne, så vores lærer kan se om det er blevet forstået. Men den skærer ikke i (3,4) toppunktet ligger dog på (1,1)

Brugbart svar (2)

Svar #15
15. juli 2017 af Soeffi

#5
f´(1) = 0 ⇒ 2·a·1 + b = 0 ⇔ 2a + b = 0 ⇔ b = -2a

f(1) = 1 ⇒ a·1² + b1 + c = 1 ⇔ a + b + c = 1 ⇒ c = 1 - a - b ⇔ c = 1 - a - (-2a) ⇔ c = 1 + a

f(3) = 4 ⇒ a·3² + b·3 + c = 4 ⇔ 9a + 3b + c = 4 ⇒ 9a + 3(-2a) + (1+a) = 4 ⇔ 4a = 3 ⇔ a = 3/4

Dermed er: a = 3/4, b = -2·(3/4) = -2/3 og c = 3/4 + 1 = 7/4.

Svar #16
15. juli 2017 af lottehvorerduhenne (Slettet)

Jeg kan ikke finde ud af om jeg gør noget galt her?

Vedhæftet fil:Skærmbillede 2017-07-15 kl. 21.42.50.png

Brugbart svar (0)

Svar #17
15. juli 2017 af fosfor

#16 der er taste fejl i #15, jeg får i hvert fald b=-3/2

Brugbart svar (0)

Svar #18
15. juli 2017 af Soeffi

#17 Det er rigtigt, der skal stå... b = -2·(3/4) = -3/2...

Brugbart svar (0)

Svar #19
15. juli 2017 af SuneChr

En alternativ betragtning:
Da toppunktet = (1 ; 1) og (3 ; 4) ligger på kurven, må (- 1 ; 4) også ligge på kurven p.g.a symmetri m.h.t. toppunktet.
Man har så tre ligninger med tre ubekendte.

Brugbart svar (0)

Svar #20
16. juli 2017 af fosfor

En parabel med toppunkt i (0, 0) er
$a\cdot x^2$

Flyt (0, 0) til (1, 1):
$a\cdot (x-1)^2+1$

Indsæt x=3, sæt lig 4 og isoler a:
$a\cdot (3-1)^2+1=4 \Rightarrow a=3/4$

Dvs.
$f(x)=3/4\cdot (x-1)^2+1$

Forrige 1 2 Næste

Der er 21 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.