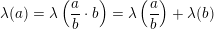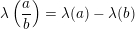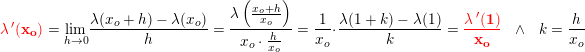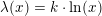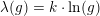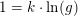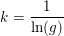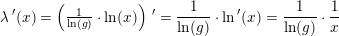Matematik

Logaritmer

14. august 2017 af SNBryce - Niveau: A-niveau

hej,

sidder med spørgsmålet

Gør rede for logaritmer og forklar om differentiation og grafiske egenskaber for denne type funktioner??

Men jeg forstår ikke hvad det er jeg skal gøre og hvordan jeg skal vise det?

Brugbart svar (0)

Svar #1
14. august 2017 af mathon

For en logaritmefunktion 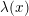$\small \lambda (x)$ med grundtal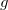 $\small g$
gælder:
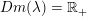
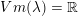
$\small Dm(\lambda )=\mathbb{R}_+$ $\small Vm(\lambda )=\mathbb{R}$

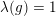
$\small \lambda (g)=1$

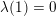
$\small \lambda (1)=0$

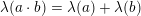
$\small \lambda (a\cdot b)=\lambda (a)+ \lambda (b)$

Logaritmefunktioner er proportionale:

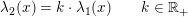
$\small \lambda_2 (x)=k\cdot \lambda_1 (x)\; \; \; \; \; \; \; k\in\mathbb{R}_+$

For den naturlige logaritmefunktion 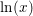$\small \ln(x)$ med grundtal $\small e$
gælder:
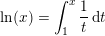
$\small \ln(x)=\int_{1}^{x}\frac{1}{t}\, \mathrm{d}t$

gælder:
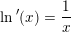$\small \ln{'}(x)=\frac{1}{x}$ og dermed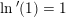 $\small \ln{'}(1)=1$

Brugbart svar (0)

Svar #2
14. august 2017 af mathon

differentiation:

Til brug i det følgende:
$\small \small \lambda (a)=\lambda \left ( \frac{a}{b}\cdot b \right )=\lambda \left ( \frac{a}{b} \right )+\lambda (b)$
hvoraf:
$\small \lambda \left ( \frac{a}{b} \right )=\lambda (a)-\lambda (b)$

$\small \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \mathbf{\color{Red} \lambda{\, }' (x_o)}=\underset{h\rightarrow 0}{\lim} \frac{\lambda (x_o+h)-\lambda (x_o)}{h}=\frac{\lambda\left ( \frac{x_o+h}{x_o} \right )}{x_o\cdot \frac{h}{x_o}}=\frac{1}{x_o}\cdot \frac{\lambda (1+k)-\lambda (1)}{k}=\mathbf{\color{Red} \frac{\lambda{\, }'(1)}{x_o}}\; \; \;\wedge\; \; \; k=\frac{h}{x_o}$

Brugbart svar (0)

Svar #3
14. august 2017 af mathon

og:

$\small \lambda (x)=k\cdot \ln(x)$

$\small \lambda (g)=k\cdot \ln(g)$

$\small 1=k\cdot \ln(g)$

$\small k=\frac{1}{\ln(g)}$

$\small \lambda {\, }'(x)=\left (\tfrac{1}{\ln(g)}\cdot \ln(x) \right ){\, }'=\frac{1}{\ln(g)}\cdot \ln{ }'(x)=\frac{1}{\ln(g)}\cdot \frac{1}{x}$

Svar #4
14. august 2017 af SNBryce

det første giver god mening... men så bliver jeg forvirret?

Brugbart svar (0)

Svar #5
14. august 2017 af fosfor

Fra potensreglerne har vi:
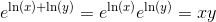
$e^{\ln(x)+\ln(y)}=e^{\ln(x)}e^{\ln(y)}=xy$

Tag ln på begge sider:
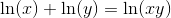
$\ln(x)+\ln(y)=\ln(xy)$

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Lad:
$g(x)=e^x\quad,\quad y=\ln(x)\quad,\quad k=\ln(x+h)-\ln(x)$

Når h går mod 0, så bliver k også 0.
Derfor fås ved at differentiere:
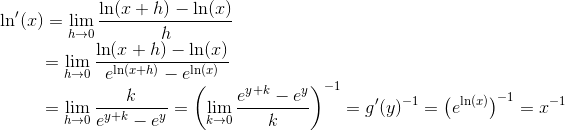
$\\\ln'(x)=\lim_{h\to 0}\frac{\ln(x+h)-\ln(x)}{h} \\ \left.\right.\quad\quad = \lim_{h\to 0}\frac{\ln(x+h)-\ln(x)}{e^{\ln(x+h)}-e^{\ln(x)}} \\ \left.\right.\quad\quad = \lim_{h\to 0}\frac{k}{e^{y+k}-e^{y}} = \left(\lim_{k\to 0}\frac{e^{y+k}-e^{y}}{k} \right)^{-1} = g'(y)^{-1}=\left(e^{\ln(x)} \right )^{-1}=x^{-1}$

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Tilsvarende resultater følger for logaritmer med andet grundtal, b, ved at definere disse som
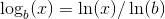
$\log_b(x)=\ln(x)/\ln(b)$

Svar #6
14. august 2017 af SNBryce

forstår godt, hvad du skriver - men hvor kommer det fra ??

lad: g(x)=...... ??

kan man ikke tegne sådan noget

Brugbart svar (0)

Svar #7
14. august 2017 af fosfor

Sekanthældningen for e^x dukker op midt i differentationen, hvorfor det er praktisk med notationen:
lad: g(x)=.....

Jeg kender ikke et tegnebevis for formlen for hældningen.

Brugbart svar (0)

Svar #8
14. august 2017 af mathon

#5 og #6
forudsætter at du begynder med at definere den inverse funktion til 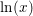$\small \ln(x)$ dvs en invers funktion til en funktion, du ikke har defineret.

Jeg er udmærket klar over, at visse matematikbøger gør det for at 'spare' papirkrævende udredninger.

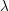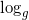Hvis det er $\small \lambda$ 'et, der forvirrer, kan du jo erstatte dem med $\small \log_g$ .

Hvad forvirrer dig?

Brugbart svar (0)

Svar #9
14. august 2017 af mathon

Det bemærkes at 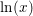$\small \ln(x)$ er defineret som den logaritmefunktion for hvilken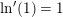 $\small \ln{}'(1)=1$
og der bringes en rettelse:

Logaritmefunktioner er proportionale:

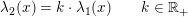
$\small \lambda_2 (x)=k\cdot \lambda_1 (x)\; \; \; \; \; \; \; k\in\mathbb{R}_+$
skal rettes til

Logaritmefunktioner er proportionale:

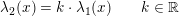
$\small \small \lambda_2 (x)=k\cdot \lambda_1 (x)\; \; \; \; \; \; \; k\in\mathbb{R}$

Svar #10
14. august 2017 af SNBryce

tror både tegn og fremgangsmåde forvirrer mig... kan ikke rigtig følge med i hvorfor

Brugbart svar (0)

Svar #11
14. august 2017 af fosfor

#5 forudsætter eksistens af en tosidet inverse til e^x

#1 forudsætter i stedet at egenskaberne i linje 2-5 gør λ veldefineret.

Brugbart svar (0)

Svar #12
14. august 2017 af mathon

Grafiske egenskaber for logaritmefunktioner:

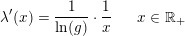
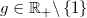
$\small \lambda {}'(x)=\frac{1}{\ln(g)}\cdot \frac{1}{x}\; \; \; \; \; \; x\in\mathbb{R}_+$ $\small g\in\mathbb{R}_+\backslash\, \{1\}$

Fortegnet
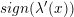$\small sign(\lambda {}'(x))$ afhænger derfor kun af fortegnet for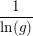 $\small \frac{1}{\ln(g)}$
hvor man har:

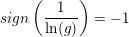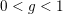$\small sign \left (\frac{1}{\ln(g)} \right )=-1$ for $\small 0<g<1$ det vil sige 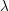$\small \lambda$ er monotont aftagende

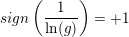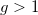$\small sign \left (\frac{1}{\ln(g)} \right )=+1$ for $\small g>1$ det vil sige 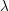$\small \lambda$ ? er monotont voksende.

Alle logaritmefunktioner skæres i 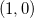$\small (1,0)$ .

Brugbart svar (0)

Svar #13
14. august 2017 af Eksperimentalfysikeren

Det bør også nævnes, at den første logaritmefunktion, der er blevet tabellagt, er 10-talslogaritmen, der blev tabellangt af Henry Briggs.

Betegnelsen logaritme stammer fra John Napier, der oprindelig fik idéen fra de trigonometriske ligninger, vi i dag kender som de logaritmiske formler. John Napier definerede en logaritmefuktion som en funktion, der opfylder funktionalligningen λ(a*b) = λ(a) + λ(b). Hans eget forsøg på at finde en sådan funktion lykkedes kun delvis. Den opfyldte ligningen f(a*b) = f(a) +f(b) + k.

Da man fandt ud af, at

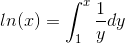
$ln(x) = \int_{1}^{x} \frac{1}{y} dy$

er en logaritmefunktion, havde man så det problem, om denne funtion var fundamentalt forskellig fra Briggs logaritme. Derfor er beviset for, at alle logaritmefunktioner er proportionale, et vigtigt bevis. ln kaldes dels den naturlige logaritme og dels Napiers logaritme. Den er beslægtet med Napiers oprindelige funktion.

Briggs logaritmer har været ekstremt vigtige op til sidste halvdel af 1900-tallet, dels direkte ved brug af tabeller, dels som fundament for regnestokken.

Derudover danner den grundlag sammenligning af lydniveauer, idet en faktor 10 mellem to lydniveauer betegnes 1 Bell. Da det er en ret stor enhed, benyttes normalt underenheden deciBell, dB, hvor 1B = 10dB. I fotografien benyttes forskellige skalaer for filmfølsomheder. Den tyske DIN-skala er også baseret på Briggs logaritmer. Analogt til dB betegner 10 trin på DIN-skalaen en faktor 10 i følsomheden.

2-talslogaritme benyttes i computerteknikken, fordi antallet af bits, der skal til at skrive et givet tal, er ca lig med 2-talslogaritmen til tallet.

I fysikken optræder ln en del, men hyppigere finder man dens inverse, exp.

Brugbart svar (0)

Svar #14
15. august 2017 af mathon

Opsummeret:
#5 er fagligt i orden men pædagogisk "uholdbar".

Skriv et svar til: Logaritmer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.