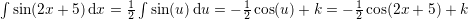Matematik
Bestem integral
Heej, hvordan løses følgende opgaver?
Svar #2
25. september 2017 af peter lind
Brug substituton
Den første t = x-4 dt=dx
Den anden
t = 2x+5 dt=2dx
Svar #4
25. september 2017 af BadBoyBard (Slettet)
Du skal bruge substitution. Det første integrale kan du også omskrive til:
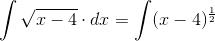
Som subsitution kunne du til den første bruge:
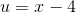
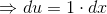
Og til den anden del:
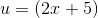
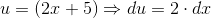
Så nu er det bare at finde integralet af:
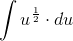
Og
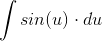
Efter du har fundet hvad disse to integraler foroven er, er det bare at sætte ind for u og du. Prøv at se, om disse råd ikke hjælper dig lidt på vej.
Mvh,
B
Svar #7
25. september 2017 af Liselotteeee
Tusind tak for hjælpen!
Har dog stadig lidt svært ved at finde integralet af u^1/2 *du.
Svar #8
25. september 2017 af BadBoyBard (Slettet)
#7: Det, du har svært ved at finde integralet af, er:
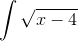
Men lad os gøre dette "step-by-step". Udtrykket foroven kunne jo også skrives som:
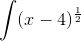
Eftersom en kvadratrod er det samme som at tage 1/2 af noget. Okay, nu kommer du nok til at have det som om, at "ej, det der x-4 gidder jeg bare ikke at se. Alt for besværligt". Og jeg er helt enig med dig der. :) Så lad os substituere og kalde x-4 for u, således at:
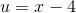
Og "du" vil så være:
![du=\frac{d}{dx}[x-4]\rightarrow du=1](https://media.studieportalen.dk/images/equations/d5Q3rQdp3qxpAtax2xN4gw==.gif)
Hvis vi kalder det der ubehaglige udtryk inde i parentesen for u, så vil vores integrale hedde:
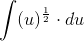
Nu er det nok meget nemmere. Det er jo bare at finde integrallet af:
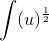
At integrere er det modsatte af at differentiere. Så hvis du integrerer noget, skal du få det du integrerede tilbage til dens orginale form, hvis du differentierer. Så skal du bare spørge dig selv, hvad skal jeg have således, at hvis jeg differentierer så vil jeg få akkurat udtrykket foroven?
Alternativt kunne du bruge denne formel:
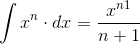
Hvis vi bruger denne formel foroven, så vil vi få, at u^1/2 bliver:
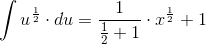
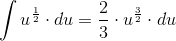
Nu er det bare at 'sætte ind' for u og du. Altså:
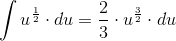
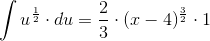
Altså er:
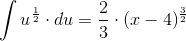
Ah, vi glemte lige et lille "C" til sidst. ;-) Husk lige at pluse med "C" hver gang du er klar til at give dit endelige svar på det du har integreret, så dit rigtige/endelige resultat bliver altså:
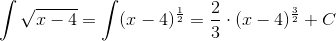
Giver dette mening for dig? Prøv evt. at beregne integralet af:
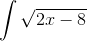
Og skriv hvad du får. Så kan jeg fortælle om det er rigtigt, således at du forstår hvordan man integrerer 100%.
Mvh,
B
Skriv et svar til: Bestem integral
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.









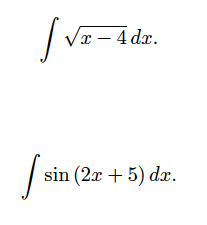
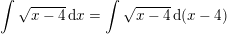
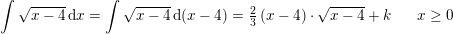
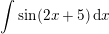
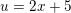 og dermed
og dermed