Matematik

Integralregning - Punktmængde og omdrejningslegeme

25. september 2017 af HannaCC (Slettet) - Niveau: A-niveau

Hej, jeg har fået stillet nedenstående opgave, men er ikke sikker på, hvordan de skal laves

Opgave:

Vi ser på punktmængden begrænset af x-aksen, grafen for f(x) = 1/x samt linjerne x = 1 og x = a, hvor a er større end 1.

1. Bestem et udtryk for arealet af punktmængden. Hvad sker der med arealet når 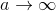$a \rightarrow \infty$ ?

2. Punktmængden drejes 360° om x-aksen. Bestem et udtryk for rumfanget af omdrejningslegemet. Hvad sker der med rumfanget, når 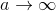$a \rightarrow \infty$ .

På forhånd tak

Brugbart svar (1)

Svar #1
25. september 2017 af fosfor

Der er tale om arealet under grafen for f(x) hvor x går fra 1 til a.

Arealet er lig
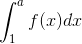
$\int^a_1f(x)dx$

Dvs. find en stamfunktion og sæt grænserne ind

Brugbart svar (1)

Svar #2
25. september 2017 af swpply (Slettet)

1) Arealet af punktmængden

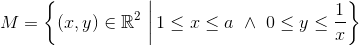
$M = \bigg\{(x,y)\in\mathbb{R}^2\ \bigg\vert\, 1\leq x\leq a\ \wedge\ 0\leq y\leq\frac{1}{x}\bigg\}$

er givet ved funktion

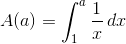
$A(a) = \int_1^a\frac{1}{x}\,dx$

2) Volumet af omdrejningslegmet er givet ved funktionen

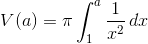
$V(a) = \pi\int_1^a\frac{1}{x^2}\,dx$

—NB. grænserne a --> ∞ er interessante.

Skriv et svar til: Integralregning - Punktmængde og omdrejningslegeme

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.