Matematik

Hjælp til trigonometri opgave

12. januar 2018 af annahansen2 - Niveau: A-niveau

Hej

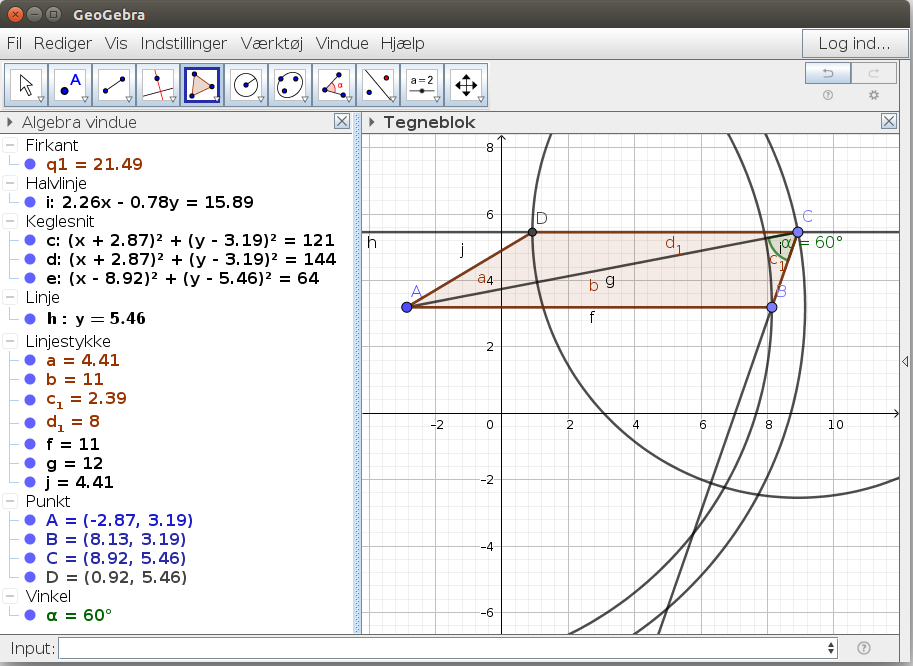
Er der nogle, der kan hjælpe med opgaven på vedhæftet billede.

Jeg har løst opgave a, men jeg har brug for hjælp til c og d. Hvilken formel kan jeg bruge til at finde længden af siden AB og arealet af et trapez?

Facit: c = 4,4. d=21,5

På forhånd tak

Vedhæftet fil: Skærmbillede 2018-01-12 kl. 19.40.49.png

Brugbart svar (0)

Svar #1
12. januar 2018 af ringstedLC

Beregn vinkel CAD. Den er lig vinkel ACB. Så har du en vinkel og to sider.

Arealet finder du i en formelsamling fx: http://www.formel.dk/Matematik/Geometri/trapez.htm

Svar #2
12. januar 2018 af annahansen2

Jeg har beregnet vinkel CAD, men jeg får ikke samme resultat som facit. Derfor spørger jeg herinde.

Er der nogle, der ved hvordan man kan beregne siden AB evt. vha. formel

Brugbart svar (0)

Svar #3
12. januar 2018 af mathon

$\small \angle ACB=10{.}87^\circ$

Svar #4
12. januar 2018 af annahansen2

Jeg har prøvet at lave nedenstående beregning

$sin(10,87)=\frac{AB}{12}=2,2$

Resultatet skal give 4,4. Hvad gør jeg forkert?

Brugbart svar (0)

Svar #5
12. januar 2018 af StoreNord

$\small \angle ACB=30^\circ$ Brug den udvidede cosinus-relation.

Brugbart svar (0)

Svar #6
12. januar 2018 af StoreNord

~~Brug appelsin-formelen på hver trekant.~~
Den foregående er også forkert

Svar #7
12. januar 2018 af annahansen2

#5, #6 Så hvilken formel skal jeg bruge?

Brugbart svar (0)

Svar #8
13. januar 2018 af StoreNord

lad mig tænke.

Brugbart svar (1)

Svar #9
13. januar 2018 af StoreNord

Ihvertfald er $\frac{11}{sin60}=\frac{12}{sinD}$ så kan du finde vinkel D

Men det havde du vel gjort.

Så kan du finde vinkel CAD. Og vinkel ACB er det samme.

Nu kan du bruge den udvide cosinus, og så videre....

Brugbart svar (1)

Svar #10
13. januar 2018 af StoreNord

Skærmbillede fra 2018-01-13 00-21-01.png

Vedhæftet fil:Skærmbillede fra 2018-01-13 00-21-01.png

Brugbart svar (1)

Svar #11
13. januar 2018 af ringstedLC

$\begin{align*} \frac{\sin (\angle D)}{\left | AC \right |}&=\frac{\sin (\angle ACD)}{\left | AD \right |} \\\\ \sin (\angle D)&=\frac{12\cdot \sin(60^\circ)}{11} \\\\ \angle D&=180^\circ-\arcsin\left ( \frac{12\cdot \sin(60^\circ)}{11} \right ),\;\angle D>90^\circ \\\\ \angle CAD&=180^\circ-(\angle ACD+\angle D) \\\\ \frac{\left | CD \right |}{\sin (\angle A)}&=\frac{\left | AD \right |}{\sin(\angle ACD)} \\\\ \left | CD \right |&=\frac{\sin (\angle A)\cdot\left | AD \right |}{\sin(\angle ACD)} \end{align}$

Brugbart svar (1)

Svar #12
13. januar 2018 af ringstedLC

$\left | AB \right |=c=\sqrt{\left | AC \right |^2+\left | BC \right |^2-2\cdot \left | AC \right |\cdot \left | BC \right |\cdot \cos(\angle ACB)}$

Brugbart svar (1)

Svar #13
13. januar 2018 af ringstedLC

c) Areal:

$\begin{align*} \frac{\sin(\angle BAC)}{\left | BC \right |}&=\frac{\sin (\angle ACB)}{\left | AB \right |} \\ \sin(\angle BAC)&=\frac{\left | BC \right |\cdot\sin (\angle ACB)}{\left | AB \right |} \\ \angle A&=\angle BAC+\angle CAD \\ Perimeter&=a+b+h\cdot\left ( \frac{1}{\sin(\theta)}+\frac{1}{\sin(\varphi)} \right ) \\ \left | AB \right |+\left | BC \right |+\left | CD \right |+\left | AD \right |&=\left | BC \right |+\left | AD \right |+h\cdot\left ( \frac{1}{\sin(\angle A)}+\frac{1}{\sin(\angle D)} \right ) \\ h&=\frac{\left | AB \right |+\left | CD \right |}{\left ( \frac{1}{\sin(\angle A)}+\frac{1}{\sin(\angle D)} \right )} \\ Areal&= \frac{1}{2}h(a+b) \\ Areal&=\frac{(\left | AB \right |+\left | CD \right |)\cdot (\left | BC \right |+\left | AD \right |)}{2\cdot \left ( \frac{1}{\sin(\angle A)}+\frac{1}{\sin(\angle D)} \right )} \\ \end{align}$

Brugbart svar (1)

Svar #14
13. januar 2018 af ringstedLC

Se tegning!

Vedhæftet fil:B_M_002_annahansen2 - Trigonometri.png

Brugbart svar (1)

Svar #15
13. januar 2018 af mathon

c)
$\small \textup{Areal:}$
$\small A_{trapez}=\tfrac{1}{2}\cdot \left | AC \right |\cdot \left | AD \right |\cdot \sin\left ( \angle CAD \right )+\tfrac{1}{2}\cdot \left | AC \right |\cdot \left | BC \right |\cdot \sin\left ( \angle ACB \right )=$

$\small \tfrac{1}{2}\cdot \left | AC \right |\cdot \left | AD \right |\cdot \sin\left ( 10{.}87^\circ \right )+\tfrac{1}{2}\cdot \left | AC \right |\cdot \left | BC \right |\cdot \sin\left ( 10{.}87^\circ \right )=$

$\small \tfrac{1}{2}\cdot \left | AC \right |\cdot \sin\left ( 10{.}87^\circ \right )\cdot \left (\left | AD \right |+ \left | BC \right | \right )=$

$\small \tfrac{1}{2}\cdot 12\cdot \sin\left ( 10{.}87^\circ \right )\cdot \left (11+8 \right )=$

$\small 6\cdot 19\cdot \sin(10{.}87^\circ)=21{.}50$

Skriv et svar til: Hjælp til trigonometri opgave

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.