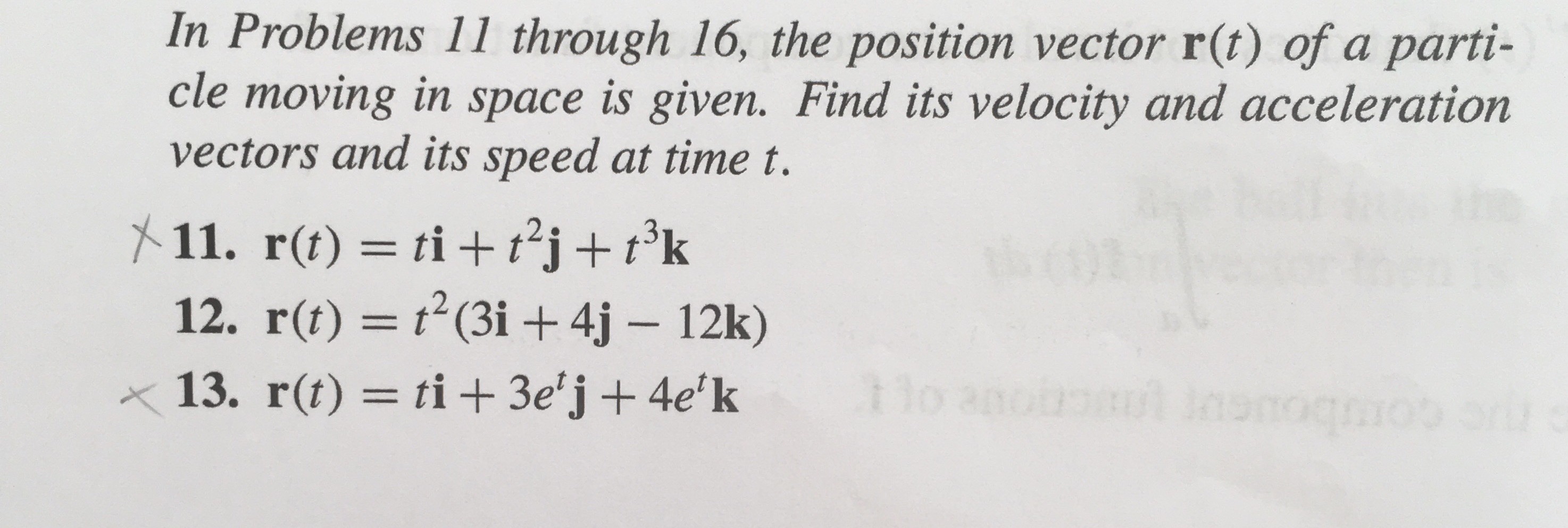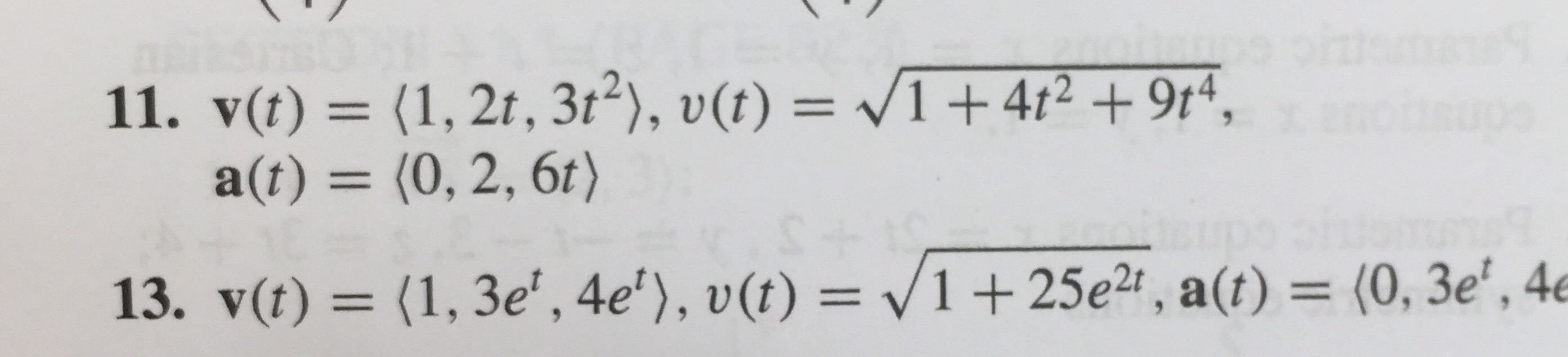Matematik

Hjælp til opgave 11 og 13

18. september 2018 af 10986 - Niveau: Universitet/Videregående

Håber at nogle har lyst til at hjælpe mig med opgave 11 og 13 ??

Vedhæftet fil: DEF3F6D5-D245-49E5-9828-0BB54BF55567.jpeg

Brugbart svar (0)

Svar #1
18. september 2018 af peter lind

Brugbart svar (0)

Svar #2
18. september 2018 af peter lind

Find r'(t) og r''(t)

Svar #3
18. september 2018 af 10986

Har du mulighed for at prøve at regne en af dem ud, så jeg kan se din fremgangsmåde? Vil nemlig virkelig gerne kunne forstå det :-)

Brugbart svar (0)

Svar #4
18. september 2018 af peter lind

r(t) = t*i+t²*j + t³* k

r'(t) = i+2t*j+3t²*k

Svar #5
18. september 2018 af 10986

Hvordan regner man sig så frem til bogens facit? ??

Vedhæftet fil:ECE2F76C-5B23-4415-9502-493FEBAE7C67.jpeg

Brugbart svar (0)

Svar #6
18. september 2018 af peter lind

Brugbart svar (0)

Svar #7
18. september 2018 af peter lind

Jeg har jo regnet den første del af første opgave. så hvad skal du egentlig have hjælp til ?

Brugbart svar (0)

Svar #8
18. september 2018 af swpply (Slettet)

BEMÆRKNING opgaven beder dig også om at bestemme farten ("speed") til tidspunktet t i hver af de to tilfælde.

Farten er pr. definition normen af hastighedsvektoren

Svar #9
18. september 2018 af 10986

Matematikken ligger mig noget bag.. Jeg tror det vil hjælpe utroligt meget med en slavisk gennemgang, med forklarende tekst til. Fordi jeg kan ikke rigtigt se hvordan jeg ender ud med at have samme facit som bogen... Mvh

Brugbart svar (1)

Svar #10
18. september 2018 af swpply (Slettet)

Vektorende $\mathbf{i},\mathbf{j},\mathbf{k}$ er de tre basis vektorer i x-,y-, og z-retningen (respektivt).

Du kan derfor skrive stedvektoren $\mathbf{r}(t)$ i opgave 11 på følgende vektor form (det er måske nemmere for dig):

$\mathbf{r}(t) = \begin{pmatrix}t\\t^2\\t^3 \end{pmatrix}$

Hastighedsvektoren $\mathbf{v}(t)$ er som bekendt defineret ved at være den afledte af stedvektoren $\mathbf{r}(t)$ , hvorfor

$\begin{align*} \mathbf{v}(t) &\equiv \frac{d}{dt}\mathbf{r}(t) \\ &= \frac{d}{dt}\begin{pmatrix}t\\t^2\\t^3 \end{pmatrix} \\ &= \begin{pmatrix}\frac{dt}{dt}\\\frac{dt^2}{dt}\\\frac{dt^3}{dt} \end{pmatrix} \\ &= \begin{pmatrix}1\\2t\\3t^2 \end{pmatrix} \end{align*}$

Accelerationsvektoren $\mathbf{a}(t)$ er ligeledes defineret ved at være den afledte af hastighedsvektoren $\mathbf{v}(t)$ , hvorfor

$\begin{align*} \mathbf{a}(t) &\equiv \frac{d}{dt}\mathbf{v}(t) \\ &= \frac{d}{dt}\begin{pmatrix}1\\2t\\3t^2 \end{pmatrix} \\ &= \begin{pmatrix}\frac{d1}{dt}\\2\frac{dt}{dt}\\3\frac{dt^2}{dt} \end{pmatrix} \\ &= \begin{pmatrix}0\\2\\6t \end{pmatrix} \end{align*}$

Farten $v(t)$ er pr. definition normen/længden af hastighedsvektoren $\mathbf{v}(t)$ , hvorfor

$\begin{align*} v(t) &\equiv \Vert\mathbf{v}(t)\Vert \\ &= \sqrt{1^2 + (2t)^2 + (3t^2)^2} \\ &= \sqrt{1+4t^2+9t^4} \end{align*}$ .

--- Prøv om du selv kan klare opgave 13.

Svar #11
18. september 2018 af 10986

Mange tak, det hjælp meget! Til sidst i opgave 13 hvor jeg skal finde hastighedsvektoren, skriver jeg det op på følgende måde:

Men kan ikke rigtigt, få det til at give samme resultalt som facit..

Vedhæftet fil:13 med facit.JPG

Brugbart svar (0)

Svar #12
18. september 2018 af peter lind

v(t) = kvrod( 1²+(3e^t)²+(4e^t)²) = kvrod(1+9e^2t+16e^2t)

Skriv et svar til: Hjælp til opgave 11 og 13

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.