Fysik

resistivitet

19. september 2018 af Nanna34 - Niveau: C-niveau

undersøge ved hjælp af regression om sammenhængen er i overstemmelse med resistivitet formlen altså om R er proportional med L

Vedhæftet fil: Screen Shot 2018-09-19 at 14.47.29.png

Brugbart svar (0)

Svar #1
19. september 2018 af swpply (Slettet)

Brugbart svar (1)

Svar #2
19. september 2018 af swpply (Slettet)

Hvad er du i tvivl omkring?? :-)

Svar #3
19. september 2018 af Nanna34

#2
Hvad er du i tvivl omkring?? :-)

om hvad de mener med at om R er proprotional med L

Brugbart svar (1)

Svar #4
19. september 2018 af PeterValberg

Resistansen R i en given leder med resistiviteten ρ og tværsnittet A er givet ved:

$R=\frac{\rho\cdot L}{A}=\frac{\rho}{A}\cdot L$

hvilket jo viser, at der er en lineær sammenhæng mellem længden L og resistansen R,
når tværsnittet A er givet og ρ jo er givet ved det pågældende ledermateriale.

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #5
19. september 2018 af mathon

   $\small y=10.35x+0.0028$
$\small \textup{er med to dec.}$
   $\small y=10.35x$
$\small \textup{dvs}$
   $\small R=\left (10.35 \; \tfrac{\Omega }{m} \right )\cdot L=\left ( \frac{\rho }{A} \right )\cdot L$

...
$\small \textup{korresponderende med:}$ https://www.studieportalen.dk/forums/thread.aspx?id=1848896#1848907

Brugbart svar (1)

Svar #6
19. september 2018 af swpply (Slettet)

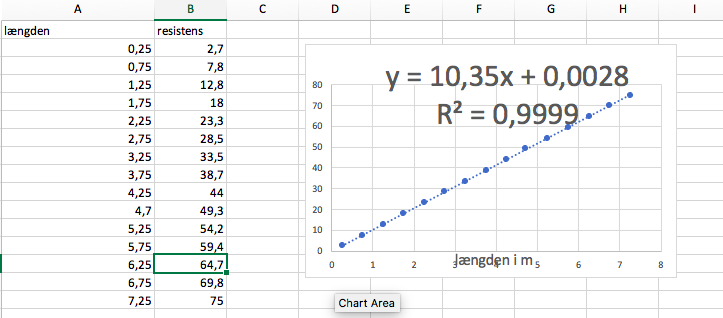
Du fortaget lineær regression på dine data og fundet at der følgende lineær sammenhæng imellem resistansen/modstanden $R$ og længden $\ell$ af en konstantantråd:

(1) $R = 10.35\tfrac{\Omega}{m}\cdot\ell + 0.0028\,\Omega$

Fra fysik timerne har du lært at du resistansen $R$ af en konstantantråd afhænger af længden $\ell$ , tværsnitsarealet $A$ på følgende måde

(2) $R = \frac{\rho}{A}\ell$

hvor $\rho$ benævner resistiviteten af den givne konstantantråd. Hvorfor at du bør forvente at resistansen $R$ er ligerem proportional med længden $\ell$ , med proportionalitetsfaktor

(3) $\frac{\rho}{A}$

Eftersom at konstantledet i (1) er forsvindende lille (og dermed kan forklares ved usikkerheder) samt at den lineære regression har R² = 0.9999 kan du slutte at du har eftervist at sammenhængen (2) er gældende inden for usikkerheden i dit forsøg. Hvad mere er, du kan besteme resistiviteten for den pågældende konstantantråd ved at observere at hældningskoefficienten i (1) nødvendigvis er givet ved (3). Du har dermed at

$\begin{align*} 10.35\tfrac{\Omega}{m} = \frac{\rho}{A} \qquad\Longleftrightarrow\qquad \rho &= 10.35\tfrac{\Omega}{m}\cdot A \\ &= 10.35\tfrac{\Omega}{m}\cdot\pi\bigg(\frac{d}{2}\bigg)^2 \\ &= 10.35\tfrac{\Omega}{m}\cdot\pi\bigg(\frac{0.25\,mm}{2}\bigg)^2 \\ &= 5.1\cdot10^{-7}\,\Omega m \end{align*}$

Skriv et svar til: resistivitet

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.