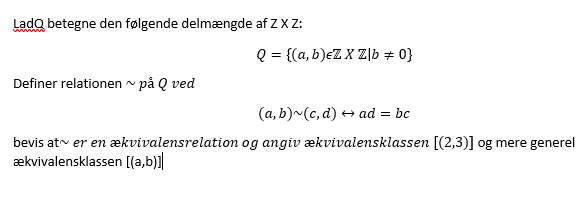Matematik
delmængde. ækvivalensklasse
hej
er der en herinde der kan hjælpe mig med denne her opgave. Jeg ved ikke hetl hvordan jeg skal gå i gang med den
Svar #2
17. oktober 2018 af swpply (Slettet)
Du skal begynde med at vise at realtionen på
er en ækvivalensrelation. Du skal altså vise at
er
1. refleksiv (trivel)
2. symmetrisk (multiplikation på er kommutativt)
3. transitiv (for ved transitivitet af relationen "=")
Svar #3
17. oktober 2018 af swpply (Slettet)
Lad være et arbitrært valgt element. Da gælder der at
Hvorfor at
.
Dette ræsonnement kan du nemt generalisere til at konkludere at
for .
Svar #4
17. oktober 2018 af swpply (Slettet)
Tilføjelse til #3. Sidste resultat er også sand såfremt at .
Svar #5
17. oktober 2018 af swpply (Slettet)
Refleksiv
Lad være et arbitrær valgt element, da gælder der
hvilket er sandt eftersom at multiplikation på er kommutativ.
Symmetrisk
Lad og
være et arbitrær valgte elementer, da gælder der
eftersom at multiplikation på kommutativ samt at "=" er symetrisk.
Transitiv
Prøv om du selv kan vise dette på tilsvarende vis som i ovenstående to tilfælde.
Svar #6
17. oktober 2018 af Eksperimentalfysikeren
#3 (4,2) er også ækvivalent med (2,1) ifølge definitionen, men [(4,2)] = {(4n,2n)|n∈Z\{0}} indeholder ikke (2,1).
Det skal nok være: [(a,b)] = {(a*n/gcd(a,b),b*n/gcd(a,d))|n∈Z\{0}}, hvor gcd(a,b) er største fælles divisor for a og b.
Svar #7
18. oktober 2018 af sajana
hvordan gør man det med transitavtiv? hvad vil det sige at den er transitiv?
Svar #9
19. oktober 2018 af swpply (Slettet)
#6 ja det er selvfølgelig rigtig. Jeg var tydeligvis lidt for hurtig i udfærdigelsen af besvarelsen i #5.
Der gælder selvfølgelig generalt at
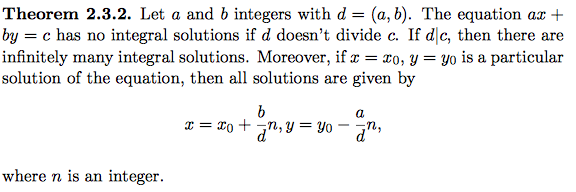
Svar #13
19. oktober 2018 af sajana
og har du eventuelt mulighed for at forklare #9 tror ikke jeg forstår det
Svar #14
19. oktober 2018 af swpply (Slettet)
#11men er den transitative så også sand?
Ja, har også den transitive egenskab. Se bevis for theorem 25 i svar #10.
#13og har du eventuelt mulighed for at forklare #9 tror ikke jeg forstår det
Ja, først skal jeg bemærke at jeg har lavet et tastefejl i #9. Istedet for at skrive "[...] besvarelsen i #5." skulle der havde stået "[...] besvarelsen i #3.".
Du skal bruge theorem 2.3.2 i #9 til bestemmelsen af den generalle restklasse [(a,b)].
Lad (x,y) ∈ Q være et tilfældigt valgt element, da gælder der at
(1)
har (iflg. theorem 2.3.2 i #9) løsninger idet at den største fælles divisor for a og b trivielt går op i 0 (Husk at samtlige tal går op i nul, med undtagelse af nul selv). Observer nu at (x,y) = (0,0) er én triviel løsning til (1), hvorfor at theorem 2.3.2 i #9 giver os at
er samtlige løsninger til (1) for .
Bruger vi nu at der for (x,y) ∈ Q bl.a. skal gælde at y ≠ 0 har vi hermed vist at
præcist som Eksperimentalfysikeren i #6 var så venlig at bemærke ;-)
Svar #17
19. oktober 2018 af sajana
tusind tak lige et spørgsmål. Der står at man skal bevise ~ er en ækvivalensrelation. Hvordan gør man det ?
Svar #19
19. oktober 2018 af swpply (Slettet)
#17
Der står at man skal bevise ~ er en ækvivalensrelation. Hvordan gør man det ?
>>>>> SE THEOREM 25 <<<<<

Svar #20
19. oktober 2018 af swpply (Slettet)
#18kan du eventuelt uddybe #16
Følgende er ikke noget bevis for påstanden i #16.
Det forekommer mig at du ikke rigtig har nogen intuation omkring ækvivalensrelationen på
. Observer følgende
Der er altså tale om rationale tal, hvorfor at betingelsen selvfølgelig er nødvendig. Mere præcist siger ækvivalensrelationen at
såfremt at det to rationale tal
er identiske
, det kunne f.eks være talene
og
.
Hvorfor bl.a. at ækvivalensklassen kan "beskrives" ved mængden
–– Jeg håber at dette giver dig en fornemelse af hvilken størrelse og
er.