Matematik

HJÆLP med andengradspolynomier

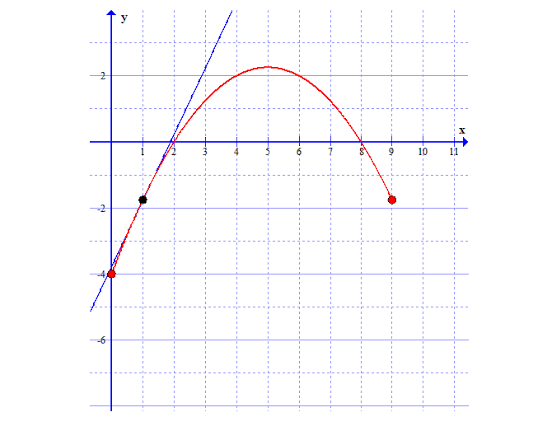
20. april 2019 af Missippi - Niveau: C-niveau

Redegør for fortegnene for a, b og c på det ovenfor viste andengradspolynomium.

b) Aflæs definitionsmængden for funktionen

c) Aflæs x-koordinaten til andengradspolynomiets rødder

d) Aflæs andengradpolynomiets toppunkt. Husk at et punkt både har en x- og en y-koordinat.

e) Aflæs andengradspolynomiets monotoniintervaller.

På grafen er indtegnet en tangent gennem punktet (1; f(1)):

f) Aflæs tangents hældningskoefficient (= væksthastighed i punktet)

g) Aflæs x-koordinaten til det punkt på grafen, hvor en tangent vil have hældningskoefficienten -1.

Vedhæftet fil: andengradspolynomier.png

Brugbart svar (0)

Svar #1
20. april 2019 af StoreNord

Tror du virkelig ikke, der er noget af det, du kan lave selv?

Svar #2
20. april 2019 af Missippi

Hej igen #1

Nej det tror jeg desværre ikke. Jeg har brugt 6 uger på dem, prøvet x antal gange.
Jeg har læst alt materiale, prøvet og fejlet. Jeg har sågår overvejet at opgive matematikken
helt og overveje ny uddannelse, da det volder mig så mange problemer.

Vh

Brugbart svar (0)

Svar #3
20. april 2019 af mathon

Brugbart svar (2)

Svar #4
20. april 2019 af mathon

$\small \small \begin{array}{llllclcl} &a<0&\textup{parabelgrenene vender nedad}\\&b>0&\textup{da tangenten har positiv differentialkvotient i (0,-4)}\\&c<0&\textup{da parablens sk\ae ringspunkt med y-aksen ligger under x-aksen}\\\\ b)&Dm(f)=\left [ 0;9 \right ]\\\\ c)&\textup{r\o dder }&x=\left\{\begin{matrix} 2\\8 \end{matrix}\right.\\\\ d)&\textup{toppunkt}&T=\left ( 5\,, \frac{9}{4} \right )\\\\ e)&f(x)\textup{ er voksende for }&0\leq x\leq 5\\ &f(x)\textup{ er aftagende for }&5\leq x\leq 9\\\\ f)&\textup{afl\ae st} f{\, }'(1)\textup{ til 2}\\\\ g)&\textup{afl\ae st} f{\, }'(7)\textup{ til -1} \end{array}$

Brugbart svar (0)

Svar #5
20. april 2019 af StoreNord

a)   Hvis jeg ikke husker helt galt er:
            a negativ, fordi det er en sur graf
            b hældningen, hvor parablen skærer y-aksen
            c hvor parablen skærer y-aksen

Skriv et svar til: HJÆLP med andengradspolynomier

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.