Matematik

Bevis for normalfordelingens maksimum er i middelværdien

28. maj 2019 af Alexander231 - Niveau: A-niveau

Kære jer,

Jeg har fået opgaven at bevise, at normalfordelingens maksimum er lig middelværdien (opgaven er vedhæftet). Jeg synes ikke umiddelbart at kunne finde løsningen i min lærebog, så jeg krydser fingre for, at I har nogle tips, tricks eller måske et tilsvarende bevis.

Hav det super, og som altid, tak for hjælpen

Vedhæftet fil: Skærmbillede 2019-05-28 kl. 15.48.32.png

Brugbart svar (2)

Svar #1
28. maj 2019 af oppenede

Eksponentialfunktionen e^x er monotont voksende, og derfor er det en og samme x-værdi der maksimerer
e^{-((x-μ)/σ)^2} vel som -((x-μ)/σ)^2

Sidstnævnte er et andengradspolynomium, med a = -1/σ², så grenene vender nedad.
Dvs. toppunktet, som er x = μ, er den x-værdi hvor maksimum antages.

Når e^{-((x-μ)/σ)^2} ganges med en positiv konstant ændrer det ikke ved hvad der er maksimum.

Brugbart svar (4)

Svar #2
28. maj 2019 af AMelev

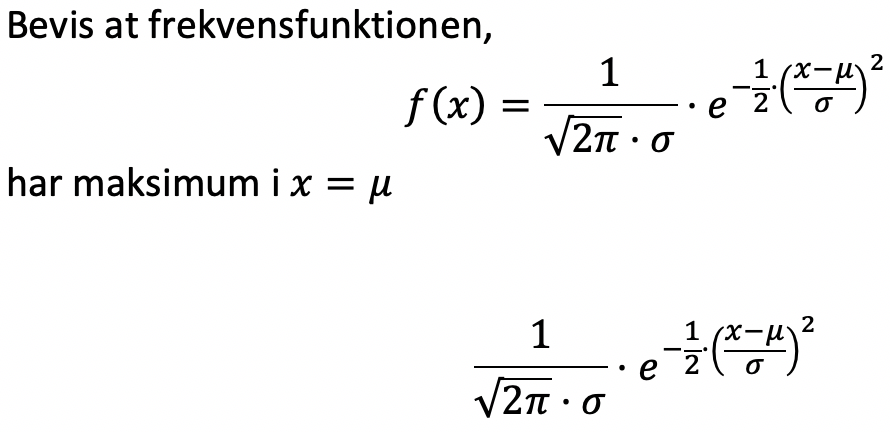
Du skal læse ordlyden omhyggeligt. Du skal ikke vise, at max(f) = μ, men at max(f) = f(μ), altså at μ er max-punkt.
Eksponenten $-\frac{1}{2}\cdot (\frac{x-\mu }{\sigma})^2= -\frac{1}{2}\cdot \frac{(x-\mu)^2 }{\sigma^2}= -\frac{1}{2\cdot \sigma^2}\cdot (x-\mu )^2$
Dermed får du $f(x)=e^{e^{ -\frac{1}{2\cdot \sigma^2}\cdot (x-\mu )^2}}=(e^{-\frac{1}{2\cdot \sigma^2}})^{(x-\mu )^2}$

Sæt $a=e^{-\frac{1}{2\cdot \sigma^2}},\: \: b=\frac{2}{\sqrt{2\pi}\cdot \sigma}\: \: \textup{og}\: \: t={(x-\mu )}^2$ , så har du $f(t)=b\cdot a^t$ , hvor a < 0 og t ≥ 0.
Altså er f aftagende, og max fås i endepunktet ved t = 0 ⇔ x = μ.

Alternativt kan du finde nulpunkter for den afledede, men så vil jeg foreslå, at du tager udgangspunkt i omskrivningen til $f(x)=b\cdot a^{(x-\mu)^2}$ , så du slipper forat cykle rundt med alle konstanterne.

Svar #3
28. maj 2019 af Alexander231

Tusind tak i to! :-))

Hav det super :-)

Brugbart svar (0)

Svar #4
04. juni 2022 af dmsf

Hej, jeg sidder også med beviset, er der nogen der kan hjælpe med at uddybe bruger "oppenede's" svar, mht. andengradspolynomium, eller i det hele taget, hvordan maksimum er lig middelværdien?

Brugbart svar (1)

Svar #5
05. juni 2022 af Anders521

#4 Polynomiet kan omskrives til

hvor og . Bruges toppunktsformlen haves .

Brugbart svar (0)

Svar #6
05. juni 2022 af dmsf

Hej mange tak, jeg prøver lige at vedhæfte et billede med beviset, sig gerne til hvis du ser noget der skal rettes, eller uddybes. Men ellers er det ligemeget, mange tak for svaret :)

Brugbart svar (0)

Svar #7
05. juni 2022 af dmsf

pdf.. man kan åbenbart ikke slette indlæg

Vedhæftet fil:Konstanten 12π.pdf

Brugbart svar (0)

Svar #8
05. juni 2022 af dmsf

Billede:

Vedhæftet fil:middelværdi lig med max.png

Brugbart svar (1)

Svar #9
05. juni 2022 af Anders521

#7 Din udregninger ser i orden ud, men du er kørt ude på et sidespor. Du vil gerne vise at . I den forbindelse er inddragelse er diskriminanten ikke nødvendig. Delen af toppunktsformlen der er relevant, er udtrykket for 1. koordinaten, dvs. , den kaldes også ligningen for symmetriaksen til en parabel.

Brugbart svar (1)

Svar #10
05. juni 2022 af Anders521

#7 Da og er

Brugbart svar (1)

Svar #11
05. juni 2022 af Soeffi

#2. (Brugbart). Evt.: f(x) har maksimum, når

$e^{-\frac{1}{2}\left ( \frac{x-\mu}{\sigma} \right )^2}$

har maksimum. Dette gælder igen, når

$\left ( \frac{x-\mu}{\sigma} \right )^2$

har minimum, dvs. for x = μ, hvor man får værdien 0, da udtrykket kan ikke antage negative værdier.

Brugbart svar (0)

Svar #12
06. juni 2022 af dmsf

Okay, #Anders521 mange tak, jo kan godt se at diskriminanten og andenkoordinaten ikke er relavant. Tak begge to

Skriv et svar til: Bevis for normalfordelingens maksimum er i middelværdien

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.