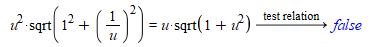Matematik

Substitutionsmetoden og kurveintegral

14. august 2019 af TeamFinal - Niveau: Universitet/Videregående

Hej SP!

Jeg sidder og bakser med en håndregningsopgave hvor jeg skal bestemme et kurveintegral ud fra funden jacobifunktion og parameterfremstilling. Parameterfremstillingn ahr jeg fået til r(u)=(u,ln(u)) hvor jacobi er sqrt(1^2+(1/u)^2) = sqrt(1+1/(u^2))

Jeg har ret svært ved at udnytte substitutionsmetoden når jeg sætter t = 1+1/(u^2), da t' = -2/(u^3).. kan jeg godt gange med -u^5/2 uden for integralet for at få det til at stemme med u^2 (som står i integralet før jacobifunktionen)?

Vedhæftet fil: sp1.PNG

Brugbart svar (0)

Svar #1
14. august 2019 af oppenede

x-intervallet har positive grænser, så x kan ganges ind i kvadratroden
$\\\int x^2 \sqrt{1+x^{-2}}\;dx=\int x \sqrt{x^2+1}\;dx \\\hspace{0cm}{\color{white}\int x^2 \sqrt{1+x^{-2}}\;dx} =\frac{1}{2}\int 2x (x^2+1)^{0.5}\;dx$
hvor 2x er den indres afledede

Svar #2
14. august 2019 af TeamFinal

hvordan får du resultatet på højre side?

Vedhæftet fil:sp2.PNG

Svar #3
14. august 2019 af TeamFinal

Ahhh, man kan sætte 1/u ud foran kvadratroden, og så bliver 1/u^2 til u^2.. og når man så sætter det udtryk sammen med u^2 ( x^2 i integralet), så bliver det til dét du har på højre siden.. den regel kendte jeg ikke! tak!

Brugbart svar (1)

Svar #4
14. august 2019 af oppenede

Den siger false fordi det ikke passer hvis u er negativ eller 0.

For positivt a kan man gange ind:
$a\sqrt{b}=\sqrt{a^2b}$

Da:
$\sqrt{a^2b}=\sqrt{a^2}\sqrt{b}=a\sqrt{b}$

Skriv et svar til: Substitutionsmetoden og kurveintegral

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.