Matematik
vektor
Hej. Hvordan skal jeg løse følgende opgave? Jeg er i tvivl om jeg skal finde hatvektor før eller efter jeg finder længden af vektorer?
mange tak på forhånd.
Svar #2
25. august 2019 af StoreNord
Er det a eller b, du spørger om?
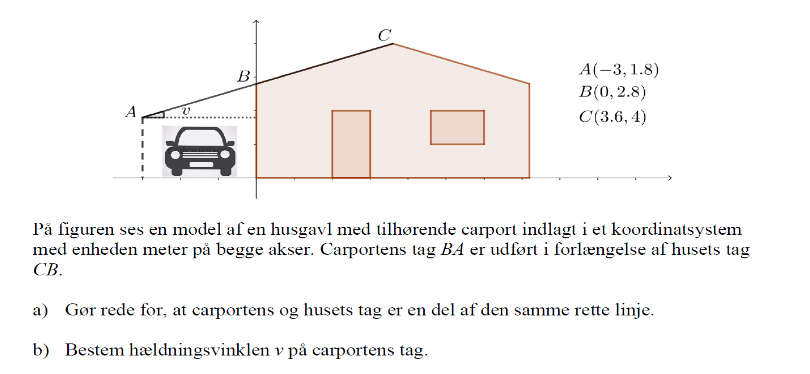
Jeg ville interessere mig for vektoren fra A til B og vektoren fra B til C.
Svar #3
25. august 2019 af Stjerneskud2016
Tak. Det er spørgsmål A. Men skal jeg først finde harvektor, før jeg finder længden af vektor?
Svar #4
25. august 2019 af ringstedLC

Tværvektor- , diff.- og skalarprodukt-formel er rigtig, men kan ikke bruges i denne opgave. Resten incl. din indledning er meget forkert.
a) Forlængelse:
b) v er vinklen mellem vektor AB og den vandrette vektor (3,0). Brug vinkelformlen.
Eller:
Svar #5
25. august 2019 af StoreNord
#3
Når du har vektor AB og vektor CB, kan du finde deres hatvektorer, og hatvektorernes skalarprodukt.
Svar #6
25. august 2019 af Stjerneskud2016
Hvad gør jeg forkert?
Svar #7
25. august 2019 af StoreNord
Jeg synes, du arbejder med for mange vektorer.
Se vedhæftede.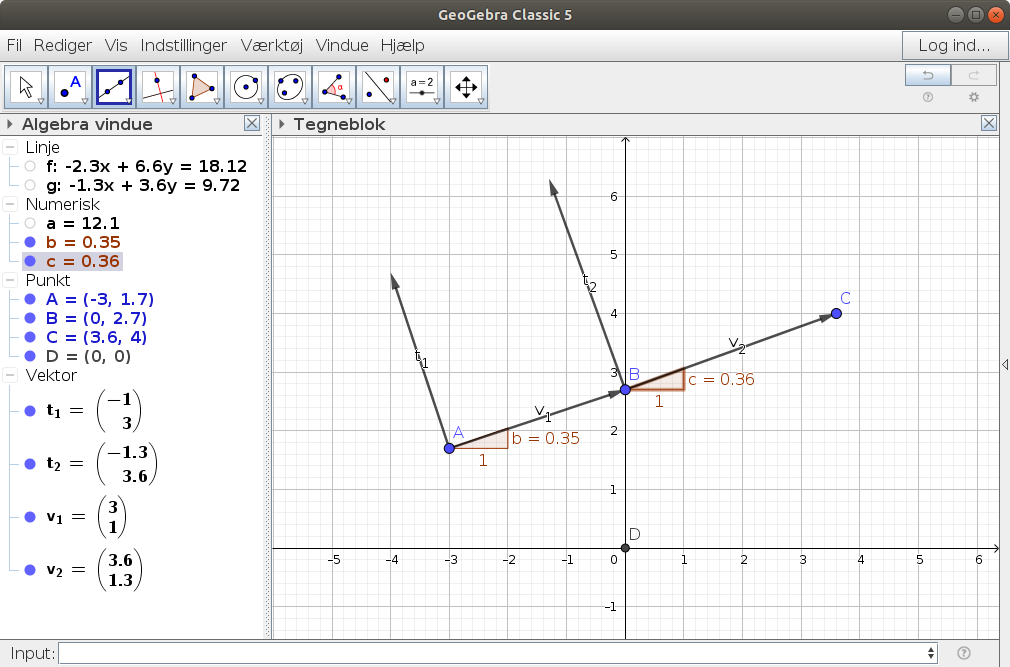
Skriv et svar til: vektor
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.