Matematik

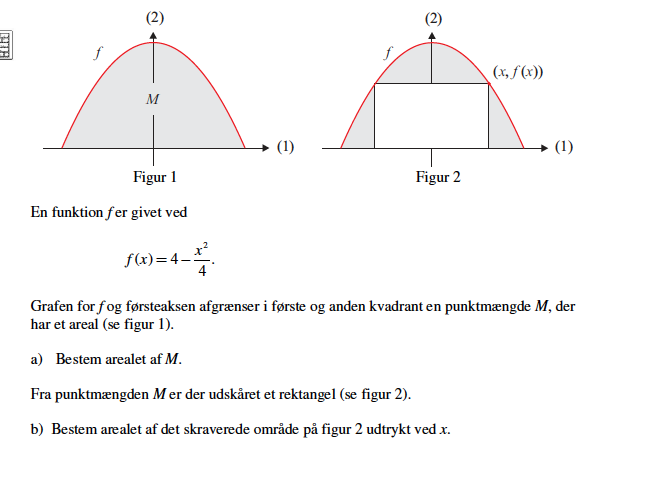
Bestem arealet af det skraverede område på figur 2 udtrykt ved x

18. september 2019 af lenemoller - Niveau: A-niveau

Jeg har regnet mig frem til opgave a, hvilket er et areal på 21,333

Men jeg kan ikke finde et udtryk for det hvide rektangel, som jeg så skal trække fra arealet af M (21,333). Er der nogen, der kan hjælpe?

Jeg har vedhæftet billede af opgaven

Vedhæftet fil: Skærmbillede 2019-09-18 kl. 20.16.56.png

Brugbart svar (0)

Svar #1
18. september 2019 af peter lind

Brugbart svar (1)

Svar #2
18. september 2019 af peter lind

rektanglens bredde er 2x og dens højde er f(x)

Brugbart svar (1)

Svar #3
18. september 2019 af StoreNord

Det hvide areal er: 2*x*f(x)

Brugbart svar (1)

Svar #4
18. september 2019 af mathon

$\small \begin{array}{lllll} \textup{Figur 1:}&A=\int_{-4}^{4} \left ( 4-\frac{x^2}{4} \right )\mathrm{d}x \end{array}$

Svar #5
18. september 2019 af lenemoller

Tak for svarene. Men hvad er arealet så er det skraverede område, jeg forstår det ikke helt?

Brugbart svar (0)

Svar #6
18. september 2019 af ringstedLC

#5: Arealet skal udtrykkes ved x, - ikke beregnes. Husk: Interval for x i udtrykket.

Svar #7
18. september 2019 af lenemoller

Hmm jeg ved den nedre grænse er -4 til den øvre grænse 4, da det er funktionens rødder, altså der hvor parablen skærer x-aksen.

Brugbart svar (0)

Svar #8
18. september 2019 af Soeffi

#0. Se evt. https://www.studieportalen.dk/Forums/Thread.aspx?id=1341409

Svar #9
18. september 2019 af lenemoller

Dvs. at udtrykket for arealet er dette nedenstående?

Arealet af skraveret område =

(64/3) - 2x • (-(1/4)x2 + 4) =

(64/3) + (1/2)x3 - 8x =

(1/2)x3 - 8x + (64/3)

Brugbart svar (1)

Svar #10
18. september 2019 af ringstedLC

#9: Du har arealet under parablen og et udtryk for arealet af rektanglet:

$\begin{align*} A_{\,skr.} &= A_{\,par.}-A_{\,rekt.} \\ A_{\,skr.} &= \int_{-4}^{4}\left (f(x) \right )-2x\cdot f(x) \\ &= \tfrac{64}{3}-2x\cdot \left ( 4-\tfrac{x^2}{4} \right ) \\ &= \tfrac{64}{3}-8x+\tfrac{2x\,\cdot \,x^2}{4} \\ &= \tfrac{64}{3}-8x+\tfrac{1}{2}x^3 \\ A_{\,skr.} &= \tfrac{1}{2}x^3-8x+\tfrac{64}{3} \\ \end{align*}$

Svar #11
18. september 2019 af lenemoller

Tusind tak for hjælpen! :)

Brugbart svar (0)

Svar #12
18. september 2019 af ringstedLC

Så glemte jeg jo lige min egen #6:

$\begin{align*} A_{\,rekt.} &= 2x\cdot f(x)\;,\;f(x)>0\Leftrightarrow -4<x<4 \;\;(f(x)=0\text{ giver ikke et rektangel}) \\ A_{\,skr.} &= \int_{-4}^{4}\left ( f(x)-2x\cdot f(x) \right )\;,\;-4<x<4 \end{align*}$

Jeg vil tro, at du kan slippe afsted med dette udtryk uden at skulle forklare, hvordan f integreres mellem nogle x-værdier for hvilke udtrykket ikke er defineret.

Skriv et svar til: Bestem arealet af det skraverede område på figur 2 udtrykt ved x

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.