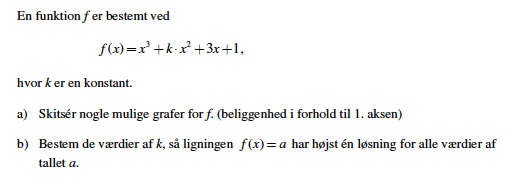Matematik

Bestem de værdier af k, så ligningen f (x)=a har højst én løsning for alle værdier af tallet a.

30. september 2019 af lenemoller - Niveau: A-niveau

Hej er der nogen, der kan hjælpe mig med denne opgave.

Vedhæftet fil: Skærmbillede 2019-09-30 kl. 20.04.30.png

Brugbart svar (0)

Svar #1
30. september 2019 af mathon

Brugbart svar (0)

Svar #2
30. september 2019 af StoreNord

Differentièr f, og sæt diskriminanten til f' lig med 0.

Brugbart svar (0)

Svar #3
30. september 2019 af mathon

Brugbart svar (0)

Svar #4
30. september 2019 af mathon

$\small \begin{array}{lllll} b)&f(x)=x^3+k\cdot x^2+3x+1\\\\ &f{\, }'(x)=3x^2+2k\cdot x+3\\\\ \textup{ekstrema:}&3x^2+2k\cdot x+3=0\\\\ &x=\left\{\begin{matrix} \frac{-k-\sqrt{k^2-9}}{3}\\\\\frac{-k+\sqrt{k^2-9}}{3} \end{matrix}\right. \\\\ \textup{dvs}\\&k<-3\quad\wedge \quad a<f\left ( \frac{-k-\sqrt{k^2-9}}{3} \right )\\\\ &k>3\quad\wedge \quad a>f\left ( \frac{-k+\sqrt{k^2-9}}{3} \right ) \end{array}$

Brugbart svar (0)

Svar #5
30. september 2019 af ringstedLC

$\begin{align*} f(x) &= a\;,\;a\in \mathbb{R}\text{ har en l\o sning}\Rightarrow f\text{ er monoton}\Downarrow \\ f'(x) &\geq 0\Updownarrow \\ 3x^2+2kx+3 &\geq 0\Updownarrow \\ d:4k^2-36 &\leq 0\Updownarrow \,\Rightarrow \text{ ingen lokale ekstrema}\\ k^2 &\leq 9\Updownarrow \\ -3&\leq k\leq 3 \end{align*}$

Svar #6
01. oktober 2019 af lenemoller

Hvorfor er det, at man skal finde f'(x) og sætte det lig med 0?

Brugbart svar (0)

Svar #7
01. oktober 2019 af mathon

Fordi lokale ekstrema bestemmes
af
$\small f{\, }'(x)=0$

Brugbart svar (1)

Svar #8
01. oktober 2019 af Bibo53

#6 Du skal ikke sætte $f'(x)=0$ . For at løse opgaven skal du gøre som følger:

1) Gør rede for, at hvis der fandtes $x_0$ så $f'(x)<0$ i en omegn på den ene side af $x_0$ og $f'(x)>0$ i en omegn på den anden side af $x_0$ så ville $f$ have et lokalt ekstremum i $x_0$ , og så ville der findes $x_1<x_0$ og $x_2>x_0$ så $f(x_1)=f(x_2)$ . Dermed ville ligningen $f(x)=a$ have mere end en løsning for $a=f(x_1)=f(x_2)$ .

2) Slut heraf, at hvis ligningen $f(x)=a$ har højst én løsning for alle $a$ , så gælder der enten $f'(x)\le 0$ for alle $x$ eller $f'(x)\ge 0$ for alle $x$ .

3) Vis at diskriminanten $d$ for andengradspolynomiet $f'$ i givet fald opfylder $d\le 0$ .

4) Vis at dette kommer ud på, at $4k^2-36\le 0$ og løs denne ulighed. Svaret kan ses i #5.

Skriv et svar til: Bestem de værdier af k, så ligningen f (x)=a har højst én løsning for alle værdier af tallet a.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.