Isolering af C

Tag udgangspunkt i:

Hvor du ved at:

Herefter vil du stå tilbage med en andengradsligning som du kan løse for at isolere C

Tak!

men vent.. C skulle gerne blive et udtryk der står i parentes opløftet i 2.
Det er ikke så vigtigt at give hvert element en værdi, da udtrykket skal bruges i R.

Mathon hvorfor plusminus tegn? Man kan vel ikke bare sådan lige fjerne en parentes, når den er opløftet i 2.?

mathon løser sådan set bare den førnævnte andengradsligning på en hurtigere måde.

plusminustegnet kommer af at bruge kvadratrod på begge sider af lighedstegnet:

Jeg tror ikke jeg forstår hvad du efterspørger. C isoleret vil altid give to udtryk?

Hvor har du fra at C kan skrives som ét udtryk kvadreret?

Maskiningeniøren> Jeg talte i tlf med min underviser i dag, som sagde, at mit udtryk for C skulle være opløftet i 2. Hvilket det jo sådan set også er. Jeg skal bare have C over på den anden side af lighedstegnet. Hvis man kan det.
Jeg har lige prøvet at løse det som en 2. gradsligning, men det bliver noget rod.

I kan godt få lov at se mine noter og tidligere udregninger samt opgaven, men det ved jeg ikke om hjælper jer. Både fordi mine noter er ulæselige og fordi opgaven er temmelig lang og indviklet.

#7 Jeg tror, det kunne være en god ide at lægge et billede af opgaven op.

Det er opgave 2bii jeg er i gang med.

Noter

Flere noter

#0

1 = (-4/β + C)²

Hvordan er du kommet frem til det udtryk? Hvad er C?
Jeg kan simpelthen ikke læse dine udregninger i den sidste fil. 
Dit udtryk K = 16e^-β·t er vist OK, men det kan jeg heller ikke helt læse.
Derfra er jeg lost. Jeg får ikke noget i retning af dit udtryk i #0 
Jeg får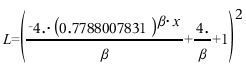 
Er det ikke meningen, at I skal bruge Maple eller et andet CAS-værktøj til at løse disse differentialligninger?

Og det er da en gang fis, at I skal skrive i hånden, fordi det skulle være besværligt at skrive matematiske symboler i tekstbehandling. Velkommen til det 21. århundrede, Ligninger i Word og Copy-paste af billeder fra andre programmer. 

AMelev: Vi bruger R. Men vi skal først bruge R, når vi kommer til 2biii.

Jeg ved ikke hvad C er. Det er det, jeg prøver at finde.
I funktion nr 3 sætter jeg 16 ind for K, som jeg fandt i 2bi, og derefter får jeg en differentialligning, som skal løses vha separation for variable.
Jeg prøver at skrive her, hvad jeg har skrevet i mine noter.

1/L^0,5 *dL = 2* e^-0,25Bt +C  dette indsættes i integral, så får jeg: (1/-0,5+1)*L^-0,5+1 = 2*(1/-0,25B)*e^-0,25Bt +C
<=> 2L^0,5 = (-8/B)*e^-0,25Bt +C <=> (det hele divideret m 2) → L=^0,5 = (-4/B)*e^-0,25Bt +C <=>
(√L)² =(-4/B*e^-0,25Bt )² <=> L = (-4/B*e^-0,25Bt +C )²
Grunden til at jeg fik det i #0 var fordi jeg satte L(0)=1
Men det er vist ikke allerede der, det skal gøres.
Og C skulle som sagt blive et udtryk opløftet i 2.

'

Nej undskyld, det er selvfølgelig C, der er 16

Og K=ce^-Bt
I  2bi altså, som skal bruges i starten af 2bii

#3 Det er ikke C, men L, der skal være et udtryk opløftet i anden (C er jo bare et tal). Det får du jo også.
Så skal du bestemme C ved at sætte t = 0 og L = 1, men gør det i denne: L^0,5 = (-4/B)*e^-0,25Bt +C , det er meget lettere. Og så får du det samme, som jeg fik.

.......<=> (det hele divideret m 2) → L=^0,5 = (-4/B)*e^-0,25Bt +C 

Der har lige sneget sig et forkert = ind

Tak, jeg fandt også selv ud af det. Og C=16 skulle åbenbart også bruges i differentialligning (3). Det var mit store problem, for jeg troede, jeg skulle finde en ny C.