Matematik

Stationære punkter

07. november 2019 af mastodont - Niveau: A-niveau

Jeg har nogle problemer med denne opgave.

Funktionen f er givet ved:

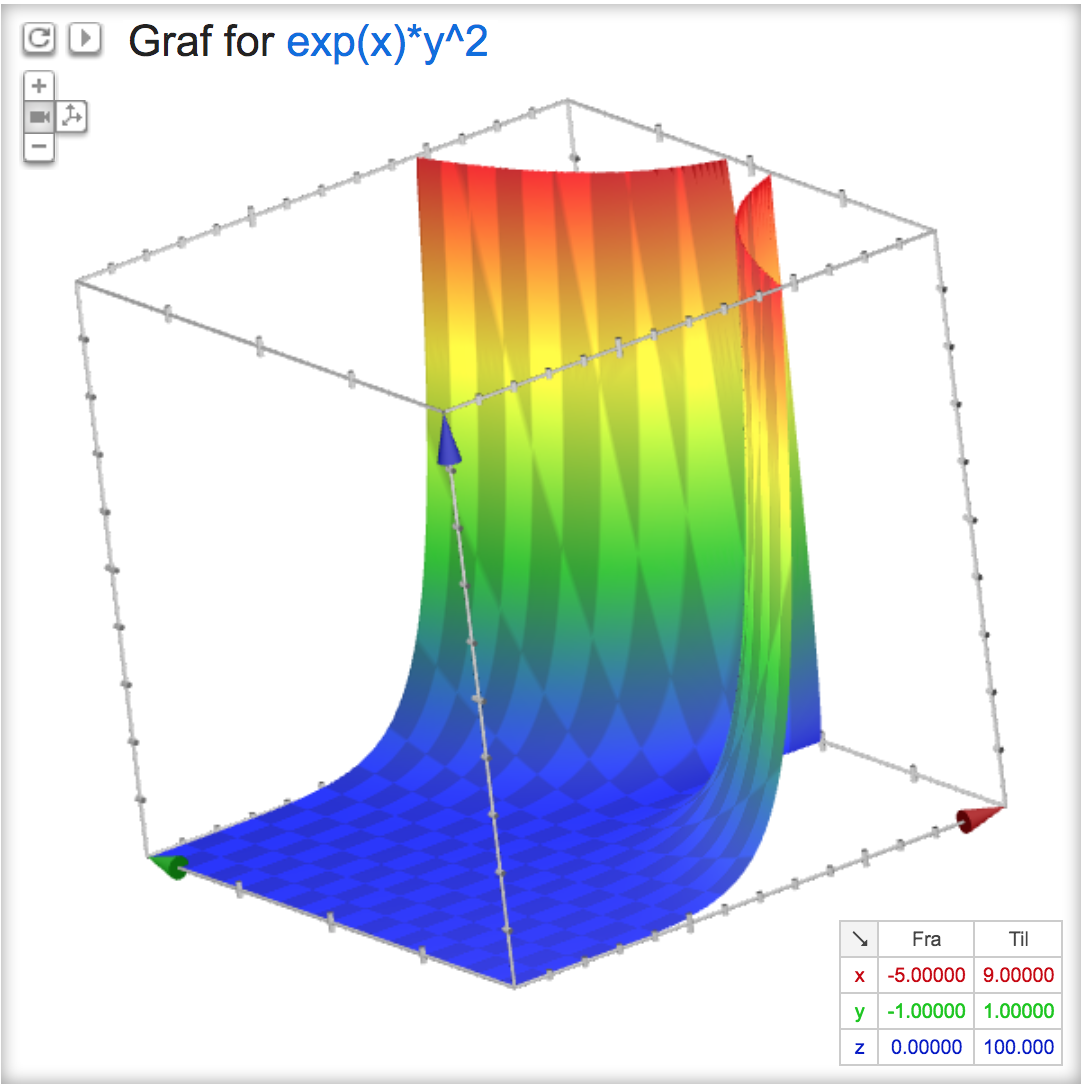
f(x,y)=e^x * y²

a. Argumenter for, at funktionen ikke har nogle stationære punkter.

Brugbart svar (0)

Svar #1
07. november 2019 af Moderatoren

Hvilke problemer har du?

Svar #2
07. november 2019 af mastodont

Jamen, jeg ved, at et stationært punkt er defineret ved, at den afledte/tangenthældningen i begge retninger er 0. Et punkt på en graf,der opfylder, at f' (x₀)=0, kaldes altså et stationært punkt.

Men jeg er i tvivl om fremgangsmåde her?

Jeg finder vel først finde de partielle afledede ved at differntiere og så sætte resultatet lig med 0 ?

Løsningerne på ligningerne angiver så antallet af de stationære punkter...

Brugbart svar (0)

Svar #3
07. november 2019 af mathon

$\small \begin{array}{llll} &f(x,y)=e^x\cdot y^2\\\\ &\frac{\partial f(x,y)}{\partial x}=f_x=y^2\cdot e^x\\\\ &\frac{\partial f(x,y)}{\partial y}=f_y=2e^x\cdot y \end{array}$

Svar #4
07. november 2019 af mastodont

Tak for svar, men kan du ikke uddybe lidt mere. hvad du gør.

Brugbart svar (0)

Svar #5
07. november 2019 af Soeffi

#0.

Vedhæftet fil:Skærmbillede 2019-11-07 kl. 16.31.53.png

Brugbart svar (0)

Svar #6
08. november 2019 af chyvak

Stationære punkter for en differentiabel funktion er punkter hvori gradienten er lig nulvektoren. Betegnelsen "stationær" kommer af, at funktionen i disse punkter hverken aftager eller vokser i nogen retning. Du skal altså bestemme de punkter, (x,y), i hvilke gradienten er nulvektoren. Gradientens komponenter er beregnet i #3. Den er identisk nulvektoren på hele x-aksen, så du har sikkert fået oplyst en defintionsmængde for f, som ikke indeholder denne.

Skriv et svar til: Stationære punkter

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.