Matematik

isoleringsproblem

12. november 2019 af bokaj123 - Niveau: A-niveau

Hej, har lidt problemer med at få k isoleret. har vedhæftet ligningen hvor jeg gerne vil have k isoleret og facit nedenunder.

Vedhæftet fil: Skærmbillede 2019-11-12 kl. 17.13.34.png

Brugbart svar (0)

Svar #1
12. november 2019 af AMelev

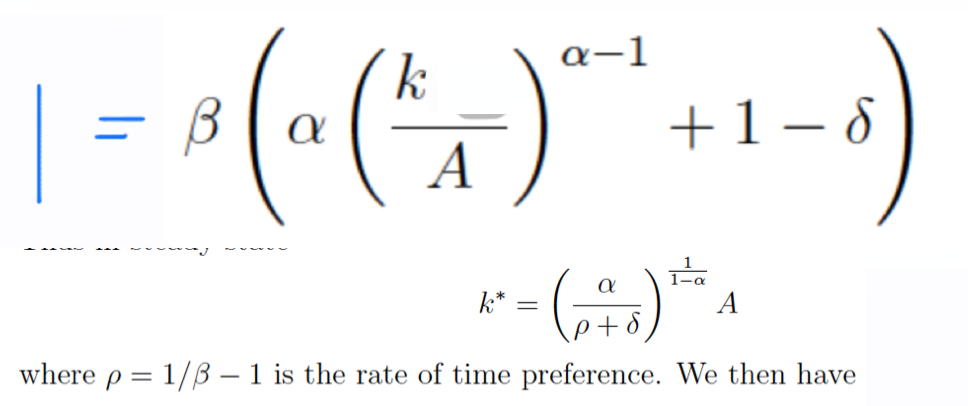
Hvad stå der på venstre side af lighedstegnet? og hvad står der i parentesen, der er opløftet i α-1?

Svar #2
12. november 2019 af bokaj123

venstre side står der 1 =

i parentesen står der (k/A)^α-1

Brugbart svar (0)

Svar #3
12. november 2019 af AMelev

$1 =\beta \cdot (\alpha \cdot((\frac{k}{A})^{\alpha -1})+1-\delta )$
Start fra en ende af og gå systematisk frem:
Dividér med β på begge sider
Træk 1 fra og læg δ til
Dividér med α på begge sider
Opløft i $\frac{1}{ \alpha -1}$   på begge sider
Gang med A  på begge sider

PS! Skriv dine opgaver ordentligt, så vi ikke behøver at skulle spilde tid på at spørge om/gætte på, hvad der skulle stå.

Svar #4
12. november 2019 af bokaj123

Hej AMelev

okay så vi har

1/β = (α(k/A)^α-1)+1-δ

1/β -1 +δ = (α(k/A)^α-1)

dividere med α

α/β - (1- δ)/α = (k/A)^α-1

opløfter med 1/a-1

(α/β - (1- δ)/α)^1/α-1 = (k/A)

ganger med A

(α/β - (1- δ)/α)^1/α-1 * A = k

synes ikke helt det ligner det i #0 men kan du måske forklare det med opløfte i 1/(α-1) ?

Brugbart svar (1)

Svar #5
12. november 2019 af AMelev

#4
1/β = (α(k/A)^α-1)+1-δ OK

1/β -1 +δ = (α(k/A)^α-1) OK

dividere med α Ja, men det gør du jo ikke

α/ (1/β - (1- δ))/α = (k/A)^α-1 Her laver du et eller andet fittelifut, hvor du ganger 1/β med α

opløfter med i 1/(a-1)

(α/β - (1- δ)/α)^1/α-1 = (k/A)

ganger med A

(α/β - (1- δ)/α)^1/α-1 * A = k OK, bortset fra, at de foregående fejl nedarves

synes ikke helt det ligner det i #0 men kan du måske forklare det med opløfte i 1/(α-1) ?

Iflg det udvidede potensbegreb er $x^{\frac{1}{n}}=\sqrt[n]{x}$ ?, så når du skal ophæve potensen (α-1) i .... ^α-1 skal du tage $\sqrt[\alpha -1]{...}= (...)^{\frac{1}{\alpha -1}}$

$\frac{1}{\beta } = \alpha \cdot((\frac{k}{A})^{\alpha -1})+1-\delta \Leftrightarrow \frac{1}{\beta }-1+\delta = ((\frac{k}{A})^{\alpha -1})\Leftrightarrow$
$\frac{\frac{1}{\beta }-1+\delta }{\alpha}=(\frac{k}{A})^{\alpha -1}\Leftrightarrow (\frac{\frac{1}{\beta }-1+\delta }{\alpha})^{\frac{1}{\alpha -1}}=\frac{k}{A}\Leftrightarrow k= A\cdot (\frac{\frac{1}{\beta }-1+\delta }{\alpha})^{\frac{1}{\alpha -1}}$

Derefter kan du så buge, at $(...)^{\frac{1}{\alpha -1}}= (...)^{\frac{-1}{1-\alpha }}=(\frac{1}{...})^{\frac{1}{1-\alpha }}$ , da $a^{-n=\frac{1}{a^n}}$ iflg. det udvidede potensbegreb.

Svar #6
13. november 2019 af bokaj123

tak for svaret, ved ikke helt hvad der gik galt, tror jeg tænkte at når man dividere ind i en brøk er det det samme som at gange tælleren, men tydeligvis ikke!

Derefter bruger vi def: 1/beta = 1-rho. , men hvordan kommer man frem til #0 løsningen ved det?

Svar #7
13. november 2019 af bokaj123

okay nu kan jeg se løsningen.. hold da op det var meget man skulle igennem ...

Svar #8
13. november 2019 af bokaj123

så man får 1/ (.....) og da α står i nævneren og det er en brøk kan man gange den op i tælleren. det var faktisk det jeg tænkte på da jeg lavede fejlen i #4

Brugbart svar (0)

Svar #9
13. november 2019 af AMelev

#6 Når man dividerer en brøk med et tal ganger man tallet på i nævneren eller dividerer i tælleren - hvis det går op (det svarer til at forkorte).

#8 Når man dividerer med en brøk, ganger man med den omvendte brøk (gange er jo det omvendte af dividere, så "to gange omvendt ophæver hinanden")

Svar #10
13. november 2019 af bokaj123

ja, det kan jeg godt se :) hvad med denne (se filen) har prøvet at tage n-de rod men...

Vedhæftet fil:Skærmbillede 2019-11-13 kl. 13.47.34.png

Skriv et svar til: isoleringsproblem

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.