Matematik
Vektorligninger
Hej, jeg sidder lige nu med en opgave om vektorligninger, som jeg ikke har helt nemt ved. Opgaverne kan ses på de vedhæftede filer. Jeg ved ikke meget om vektorligninger, og jeg ville derfor sætte pris på detaljerede forklaringer (jeg forsøger at hjælpe en ven på HTX, da jeg ikke selv har haft om vektorligninger på STX).
Til opgaverne er følgende informationer givet:
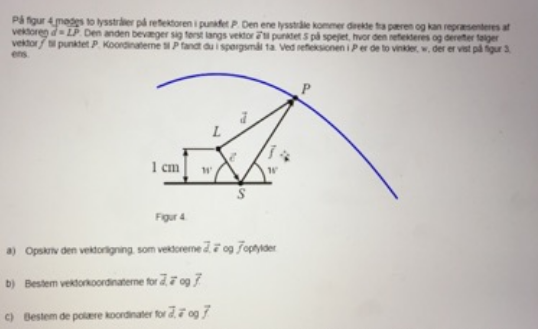
Billede 1:
Punktet L har koordinaterne (0,4)
Punktet P har koordinatsættet (2,68 , 5,29)
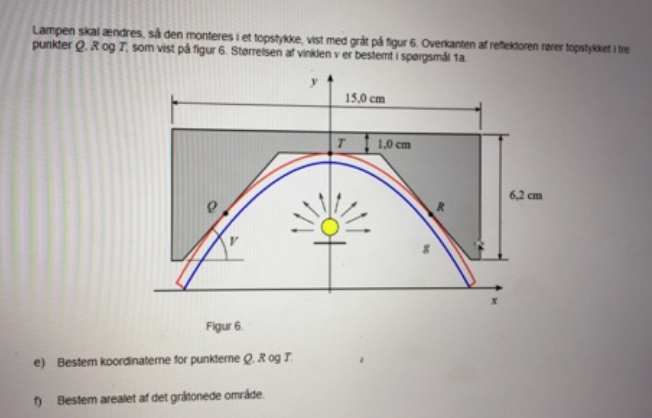
Billede 2:
Vinklen V er 50,41 grader.
Den blå graf/funktion er fundet til at være -0,1265x+6,2, og tykkelsen til den røde graf er 5 mm.
Mine spørgsmål lyder:
1: Hvordan opskriver jeg vektorligningen i opgave a på billede 1?
2: Hvordan finder jeg koordinaterne til punktet S på billede 1 (jeg ved naturligvis, at y-koordinatet til punktet er 3, og at vinklerne er lige store til begge sider, og jeg har derfor også kunnet finde mig frem til resultatet i Geogebra, men er der en anden måde at gøre det på via beregninger?)
3: Hvordan bestemmer jeg koordinaterne til punkterne Q og R på billede 2?
Den mindste smule hjælp er værdsat :-).
Svar #1
21. november 2019 af PeterValberg
Jeg indsætter lige billederne, det gør det nemmere at hjælpe
billede 1
Svar #3
21. november 2019 af chyvak
ad 1) Vektorsummen af e og f er lig d, d = e + f
ad 2) Man kunne eksempelvis udnytte at L spejlet i den lodrette normal i S(x, 3) må ligge på linien bestemt ved vektor f. Med L(0,4) må det spejlede punkt have koordinaterne L'(2x, 4). Man kan så udtrykke at hældningen af liniestykkerne SL' og L'P er den samme. Det vil give en førstegradsligning til bestemmelse af x.
ad 3) Man kunne finde de punkter på den blå kurve, hvori tangenhældningen numerisk er lig den søgte vinkel og så addere afstanden 5 mm langs normalen.
Skriv et svar til: Vektorligninger
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.