Matematik

Bestem a,b og c

01. december 2019 af Mie23234 - Niveau: A-niveau

Nogle der kan hjælpe?:)

Vedhæftet fil: Skærmbillede 2019-12-01 kl. 20.12.33.png

Brugbart svar (0)

Svar #1
01. december 2019 af StoreNord

Differentièr f og p to gange, og opstil et lignings-system med 3 ligninger med 3 ubekendte.

Svar #2
01. december 2019 af Mie23234

#1
Differentièr f og p to gange, og opstil et lignings-system med 3 ligninger med 3 ubekendte.

Når jeg differentiere p og f to gange får jeg henholdsvis:

f(x)=(x-2)*e^-x og p(x)=2*a

Er det rigtigt? og hvad skal man så?:)

Brugbart svar (1)

Svar #3
01. december 2019 af StoreNord

Nej. Sådan her:
Skærmbillede fra 2019-12-01 21-27-17.png
og opstil et lignings-system med 3 ligninger med 3 ubekendte.

Vedhæftet fil:Skærmbillede fra 2019-12-01 21-27-17.png

Svar #4
03. december 2019 af Mie23234

#3
Nej. Sådan her:

og opstil et lignings-system med 3 ligninger med 3 ubekendte.

Må jeg spørge om da du differentiere p(x) hvor a,b og c går hen, og hvordan er det nu man opstiller 3 ligninger med 3 ubekendte?:)

Brugbart svar (0)

Svar #5
03. december 2019 af StoreNord

$\\p(x) = ax^{2}+bx+c \\p'(x) = 2ax^{2-1}+b+0$

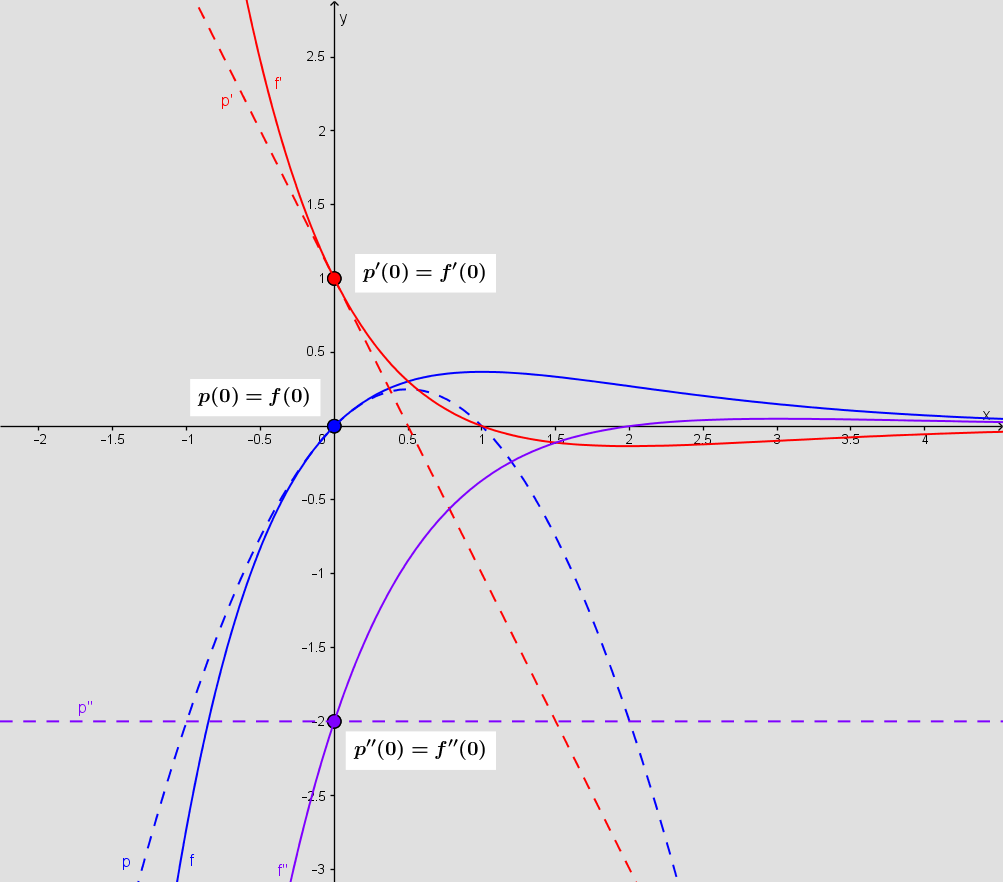
Første ligning får du ved at sætte f(0)=p(0). Altså $-0\cdot e^{-0} = -a^{2}+b\cdot 0+c$ .

I den næste bruger du de 1. afledede af funktionerne.

I den tredje bruger du de 2. afledede.

Ligesom der står i opgaven. (bare omvendt)

Brugbart svar (0)

Svar #6
03. december 2019 af ringstedLC

#4
Må jeg spørge om da du differentiere p(x) hvor a,b og c går hen, og hvordan er det nu man opstiller 3 ligninger med 3 ubekendte?:)

$\begin{align*} p(0) &= f(0)=0\Rightarrow c=0 \\ p'(0) &= f'(0)=1\;,\;f'(x)=(1-x) \cdot e^{-x} \\ p''(0) &= f''(0)=-2\;,\;f''(x)=(x-2) \cdot e^{-x} \\ p(x) &= ax^2+bx \\ p'(x) &= 2ax+b\Rightarrow b=\;? \\ p''(x) &= 2a\Rightarrow a=\;? \end{align*}$

Vedhæftet fil:__0.png

Skriv et svar til: Bestem a,b og c

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.