Matematik

Integralopgave

04. december 2019 af scientist - Niveau: A-niveau

Hvordan løser man opgave b?

Vedhæftet fil: Integral 1.png

Brugbart svar (0)

Svar #1
04. december 2019 af SuneChr

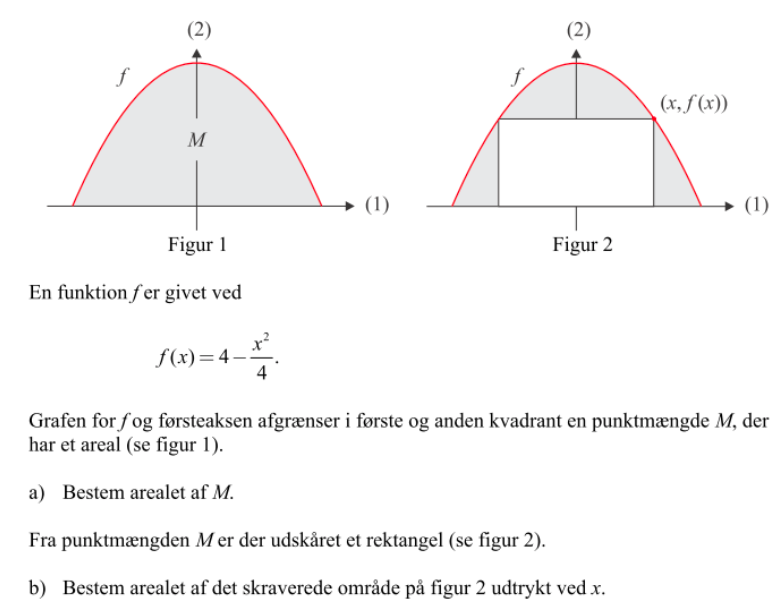
b.
Arealet af rektanglet i Fig. 2
2 · x · f (x)
skal fratrækkes arealet af punktmængden i Fig. 1.

Brugbart svar (0)

Svar #2
05. december 2019 af PeterValberg

Jeg indsætter lige billedet af opgaven, det gør det nemmere at hjælpe

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #3
05. december 2019 af mathon

Grundet symmetrien om y-aksen:

$\begin{array}{llll}a)&A_M=int_{-4}^{4}(-\frac{1}{4}x^2+4)\mathrm{d}x=2\cdot \int_{0}^{4}(-\frac{1}{4}x^2+4)\mathrm{d}x=2\cdot \left [-\frac{1}{12}\cdot x^3+4x \right ] _{0}^{4}=2\cdot \left ( -\frac{1}{12}\cdot 4^3+4^2 \right )=\tfrac{64}{3}\\\\\\\\b)&A_{skrav}=\frac{64}{3}-\left ( 8x-\frac{1}{2}x^3 \right )\\\\&A_{skrav}=\frac{1}{2}x^3-8x+\frac{64}{3}\end{array}$

Brugbart svar (0)

Svar #4
05. december 2019 af mathon

$\begin{array}{llll}b)&A_{skrav}=\frac{64}{3}-\left ( 8x-\frac{1}{2}x^3 \right )\\\\&A_{skrav}=\frac{1}{2}x^3-8x+\frac{64}{3}\qquad -4<x<4\end{array}$

Svar #5
05. december 2019 af scientist

Jeg har lige et spørgsmål, hvordan får du talllene 8x - 1/2x^3?

Brugbart svar (0)

Svar #6
05. december 2019 af mathon

$\small \begin{array}{llll}2x\cdot f(x)=2x\cdot \left ( 4-\frac{1}{4}x^2 \right )=8x-\frac{1}{2}x^3\end{array}$

Svar #7
05. december 2019 af scientist

I opgave b, hvordan skal man beregne Askrav = 64/3 - (8x -1/2x^3) skal man integere eller isolere x?

Brugbart svar (0)

Svar #8
05. december 2019 af janhaa

uten integral:

$A(parabel)=\frac{2}{3}gh\\$

Nullpkt: x=-4, x=4 => g = 4+4 = 8

f(0) = 4 = h, ergo:

$A(parabel)=\frac{2}{3}*8*4=\frac{64}{3}$

Brugbart svar (0)

Svar #9
05. december 2019 af janhaa

#7
I opgave b, hvordan skal man beregne Askrav = 64/3 - (8x -1/2x^3) skal man integere eller isolere x?

nei

Skriv et svar til: Integralopgave

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.