Matematik
Vektorfunktion
Hvordan løser man sådan en vektorfunktion?
Svar #5
07. december 2019 af Mie23234
#4
Hej Mathon, da det er med hjælpemidler er der sp en nemmere måde at gøre dette på:))
Svar #6
07. december 2019 af AMelev
Hvordan, du konkret gør, afhænger af dit CASværktøj, men
x(t) := x0+r·cos(t)
y(t) := y0+r·sin(t)
Se evt. nedenstående i Nspire-udgave:
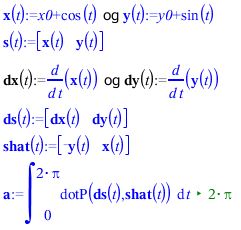
Svar #7
08. december 2019 af Mie23234
#6Hvordan, du konkret gør, afhænger af dit CASværktøj, men
x(t) := x0+r·cos(t)
y(t) := y0+r·sin(t)
Se evt. nedenstående i Nspire-udgave:
TUSIND TAK, lige det jeg mente
Skriv et svar til: Vektorfunktion
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



