Matematik

trekantsbevis

23. december 2019 af Ua123 - Niveau: B-niveau

Hej er der nogen der kan hjælpe mig med dette spørgsmål som høre til trekanten på billedet i kommentarfeltet? :)

Vedhæftet fil: 6E4F54AE-5769-4F88-A2C8-CF918785C503.jpeg

Svar #1
23. december 2019 af Ua123

Her er trekanten

Vedhæftet fil:4BB10072-F6AA-4E6B-BC0B-558EC770FA42.jpeg

Brugbart svar (0)

Svar #2
23. december 2019 af peter lind

Brugbart svar (1)

Svar #3
23. december 2019 af Soeffi

#0. Generelt:

Hvis en trekant har heltallige sider, og hvis en anden trekant er ensvinklet med denne, og hvis skaleringsfaktoren mellem dem samtidig er heltallig, så gælder at den anden trekant også har heltallige sider.

Brugbart svar (1)

Svar #4
23. december 2019 af peter lind

Brugbart svar (0)

Svar #5
23. december 2019 af peter lind

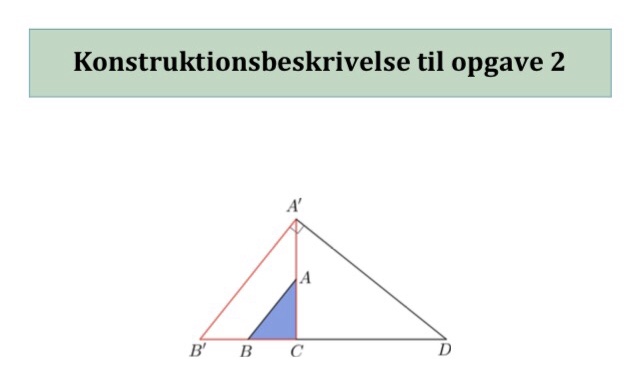
Man må også antage at B'B =BeC og A'A = AC som det ser ud til på figuren

Trekanterne ABC, A'B'C og A'B'D er ensvinklet og dermed er siderne proportionale

Brugbart svar (1)

Svar #6
23. december 2019 af StoreNord

I den lille trekant er $c^{2}=a^{2}+b^{2}$
Når alle tre sider ganges med en heltallig størrelsesfaktor, n, fås
$(nc)^{2}=(na)^{2}+(nb)^{2}$
Det er givet, at a, b og n er heltal.
Så må c også være et heltal.

Brugbart svar (1)

Svar #7
23. december 2019 af StoreNord

I #6 gik jeg ud fra, at trekanten ABC er retvinklet.
Men dèt er der jo egentlig ikke nogen, der har lovet mig.
Så måske skal der noget andet logik til.

Brugbart svar (1)

Svar #8
26. december 2019 af ringstedLC

For en retvinklet trekant med heltallige sider må der gælde:

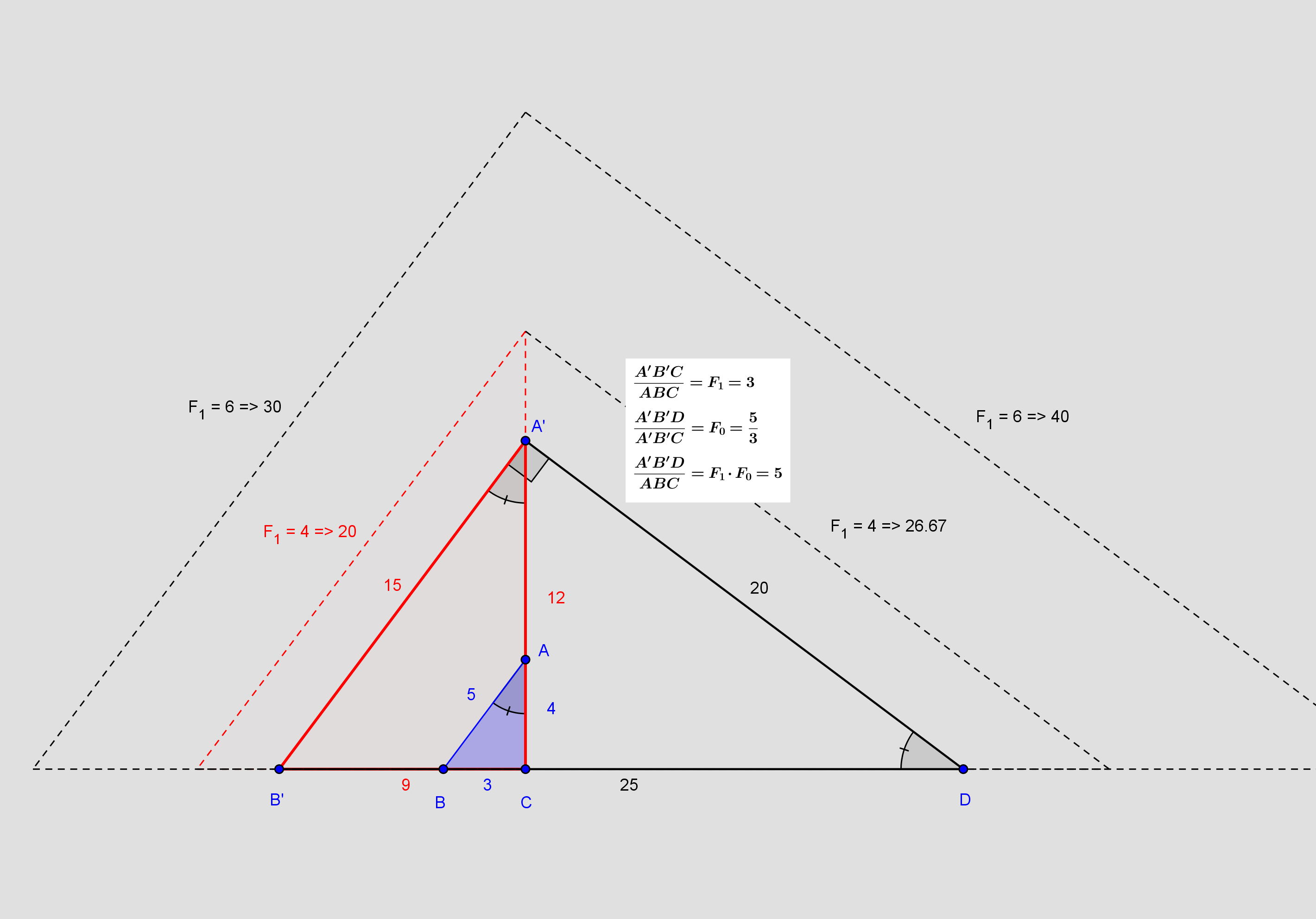
$\begin{align*} a^2+b^2 &= c^2\;,\;\left \{ a;b;c \right \} \in \mathbb{N} \\ a^2+\left (\tfrac{4}{3}a\right )^2 &= \left (\tfrac{5}{3}a\right )^2 \Downarrow \;,\;a\text{ er den korte katete i}\;\Delta ABC \\ \left \{a;\tfrac{4}{3}a;\tfrac{5}{3}a \right \} &\in \mathbb{N}\Downarrow\;,\;\tfrac{c}{a}=\tfrac{5}{3}=F_0 \\ a &\geq n\cdot 3\;,\;n \in\mathbb{N} \end{align*}$

Skalering af ΔA'B'C i forhold til ΔABC med ensliggende sider:

$\begin{align*} \Delta ABC\sim \Delta A'B'C\,&,\;\angle A=\angle B'A'C\,,\;\angle B=\angle B' \\ \frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c} &=F_1 \\ (a')^{\,2}+\left (\tfrac{4}{3}a'\right )^2 &= \left (\tfrac{5}{3}a')\right )^2 \;,\;a'\text{ er den korte katete i}\;\Delta A'B'C \\ (F_1\,a)^{\,2}+\left (\tfrac{4}{3}\,F_1\,a\right )^2 &= \left (\tfrac{5}{3}\,F_1\,a\right )^2 \Downarrow \\ F_1\,a \in \mathbb{N} &\Rightarrow F_1\in \mathbb{N} \\F_1>1 &\Rightarrow F_1\geq n\cdot 2 \\ a\geq n\cdot 3 &\Rightarrow a'\geq n\cdot 6 \end{align*}$

Det kunne se ud som ΔA'B'C er skaleret med en faktor 2.

Skalering af ΔA'B'D i forhold til ΔABC med ikke ensliggende sider:

$\begin{align*} \Delta ABC \sim \Delta A'B'D\;&,\;\angle B=\angle B'\;,\;\angle A=\angle D \\ \frac{|B'D|}{c}=\frac{|B'D|}{F_0\cdot a} &= F_0\cdot F_1 \\ |B'D| &= a\cdot {F_0}^2\cdot F_1 \\ |B'D| &\geq \tfrac{50}{3}\Rightarrow |B'D|\geq 17\;,\;|B'D| \in \mathbb{N} \\ |B'D|\geq17 \Rightarrow a\cdot {F_0}^2\cdot F_1 &\geq 17 \\ F_1 &\geq \tfrac{17\,\cdot \,9}{25\,\cdot \,3}= \tfrac{51}{25} \\ F_1 &\geq n\cdot 3\Rightarrow a'\geq {\color{Red} n\cdot 3\cdot 3=n\cdot 9} \\ a\geq n\cdot 3\Rightarrow c\geq n\cdot 5 &\Rightarrow |A'B'|\geq n\cdot 15\Rightarrow |B'D|\geq n\cdot 25 \\ \Delta ABC\overset{F_1}{\curvearrowright}\Delta A'B'C\; &,\;\Delta A'B'C\overset{F_0}{\curvearrowright}\Delta A'B'D \end{align*}$

Figuren og beregning af forholdene passer derfor ikke for godt sammen, hvis siderne skal være heltallige.

Vedhæftet fil:B_M_087 - Trekanter, ensvkl., forhold_Ua123.png

Brugbart svar (1)

Svar #9
26. december 2019 af ringstedLC

Svar #10
26. december 2019 af Ua123

#8
For en retvinklet trekant med heltallige sider må der gælde:

$\begin{align*} a^2+b^2 &= c^2\;,\;\left \{ a;b;c \right \} \in \mathbb{N} \\ a^2+\left (\tfrac{4}{3}a\right )^2 &= \left (\tfrac{5}{3}a\right )^2 \Downarrow \;,\;a\text{ er den korte katete i}\;\Delta ABC \\ \left \{a;\tfrac{4}{3}a;\tfrac{5}{3}a \right \} &\in \mathbb{N}\Downarrow\;,\;\tfrac{c}{a}=\tfrac{5}{3}=F_0 \\ a &\geq n\cdot 3\;,\;n \in\mathbb{N} \end{align*}$

Skalering af ΔA'B'C i forhold til ΔABC med ensliggende sider:

$\begin{align*} \Delta ABC\sim \Delta A'B'C\,&,\;\angle A=\angle B'A'C\,,\;\angle B=\angle B' \\ \frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c} &=F_1 \\ (a')^{\,2}+\left (\tfrac{4}{3}a'\right )^2 &= \left (\tfrac{5}{3}a')\right )^2 \;,\;a'\text{ er den korte katete i}\;\Delta A'B'C \\ (F_1\,a)^{\,2}+\left (\tfrac{4}{3}\,F_1\,a\right )^2 &= \left (\tfrac{5}{3}\,F_1\,a\right )^2 \Downarrow \\ F_1\,a \in \mathbb{N} &\Rightarrow F_1\in \mathbb{N} \\F_1>1 &\Rightarrow F_1\geq n\cdot 2 \\ a\geq n\cdot 3 &\Rightarrow a'\geq n\cdot 6 \end{align*}$

Det kunne se ud som ΔA'B'C er skaleret med en faktor 2.

Skalering af ΔA'B'D i forhold til ΔABC med ikke ensliggende sider:

$\begin{align*} \Delta ABC \sim \Delta A'B'D\;&,\;\angle B=\angle B'\;,\;\angle A=\angle D \\ \frac{|B'D|}{c}=\frac{|B'D|}{F_0\cdot a} &= F_0\cdot F_1 \\ |B'D| &= a\cdot {F_0}^2\cdot F_1 \\ |B'D| &\geq \tfrac{50}{3}\Rightarrow |B'D|\geq 17\;,\;|B'D| \in \mathbb{N} \\ |B'D|\geq17 \Rightarrow a\cdot {F_0}^2\cdot F_1 &\geq 17 \\ F_1 &\geq \tfrac{17\,\cdot \,9}{25\,\cdot \,3}= \tfrac{51}{25} \\ F_1 &\geq n\cdot 3\Rightarrow a'\geq {\color{Red} n\cdot 3\cdot 3=n\cdot 9} \\ a\geq n\cdot 3\Rightarrow c\geq n\cdot 5 &\Rightarrow |A'B'|\geq n\cdot 15\Rightarrow |B'D|\geq n\cdot 25 \\ \Delta ABC\overset{F_1}{\curvearrowright}\Delta A'B'C\; &,\;\Delta A'B'C\overset{F_0}{\curvearrowright}\Delta A'B'D \end{align*}$

Figuren og beregning af forholdene passer derfor ikke for godt sammen, hvis siderne skal være heltallige.

NICE! MANGE TAK FOR DET!!!!

Skriv et svar til: trekantsbevis

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.