Matematik

Givet tre punkter

20. januar 2020 af NW12 - Niveau: B-niveau

Halløj! Nogen som kan hjælpe med denne her opgave? Opgaven er med hjælpmidler og jeg løser den i TI-Nspire:). Tak på forhånd!

Svar #1
20. januar 2020 af NW12

Opgaven er vedhæftet

Vedhæftet fil:gds.png

Brugbart svar (0)

Svar #2
20. januar 2020 af mathon

Brugbart svar (0)

Svar #3
20. januar 2020 af mathon

$\small \small \small \small \begin{array}{lllll}a)&\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}=\begin{pmatrix} 2\\t \end{pmatrix}-\begin{pmatrix} 3\\0 \end{pmatrix}=\begin{pmatrix} 2-3\\t-0 \end{pmatrix}=\begin{pmatrix} -1\\ t \end{pmatrix}\\\\\\b)&T=\frac{1}{2}\cdot \begin{Vmatrix} -3 &-1 \\ 5& 4 \end{Vmatrix}=\frac{1}{2}\cdot \left | -3\cdot 4-5\cdot (-1) \right |=\frac{1}{2}\cdot \left | -12+5 \right |=\frac{1}{2}\cdot 7=3.5 \end{array}$

Brugbart svar (0)

Svar #4
20. januar 2020 af mathon

$\small \begin{array}{lllll}c)&\textup{At linjen gennem A og C st\aa r vinkelret p\aa \ }l\textup{ betyder, at }\overrightarrow{AC}\textup{ og }l\textup{'s retningsvektor}\\&\textup{er ortogonale.}\\&\textup{Ortogonale vektorers skalarprodukt er lig med 0.}\\\\&\begin{pmatrix} -1\\t \end{pmatrix}\cdot \begin{pmatrix} 2\\1 \end{pmatrix}=0\\\\&-1\cdot 2+t\cdot 1=0\\\\&t=2 \end{array}$

Svar #5
20. januar 2020 af NW12

Kan du vise hvordan man plotter det ind i Ti-Nspire?

Svar #6
20. januar 2020 af NW12

Skal nemlig udregne det der

Svar #7
20. januar 2020 af NW12

Forstår ikke helt b)..

Brugbart svar (0)

Svar #8
20. januar 2020 af mathon

Brug $\small \begin{bmatrix} \Box\\ \Box \end{bmatrix}$ -skabelonen

$\small \begin{array}{llll}&ac:=\begin{bmatrix} 2\\t \end{bmatrix}-\begin{bmatrix} 3\\0 \end{bmatrix} \end{array}$

Svar #9
20. januar 2020 af NW12

Kan ikke trykke enter, den siger syntaks? Hvad er forkert?

Vedhæftet fil:'ØÆLKIJHYGFD.png

Brugbart svar (0)

Svar #10
20. januar 2020 af mathon

og
$\small \begin{bmatrix} \Box&\Box\\ \Box&\Box \end{bmatrix}$

$\small abs\left ( \textup{determinant} \right )$

$\small \tfrac{1}{2}\cdot abs\left (det\left (\begin{bmatrix} -3 &-1 \\ 5& 4 \end{bmatrix} \right) \right )$

Brugbart svar (0)

Svar #11
20. januar 2020 af mathon

indtastning af skalarprodukt=Prikprodukt

$\small \textup{solve}\left (\textup{dotP}\left ( \begin{bmatrix} -1\\t \end{bmatrix},\begin{bmatrix} 2\\1 \end{bmatrix} \right )=0,t \right )$

Svar #12
20. januar 2020 af NW12

Tak!:)

Brugbart svar (0)

Svar #13
20. januar 2020 af AMelev

#9

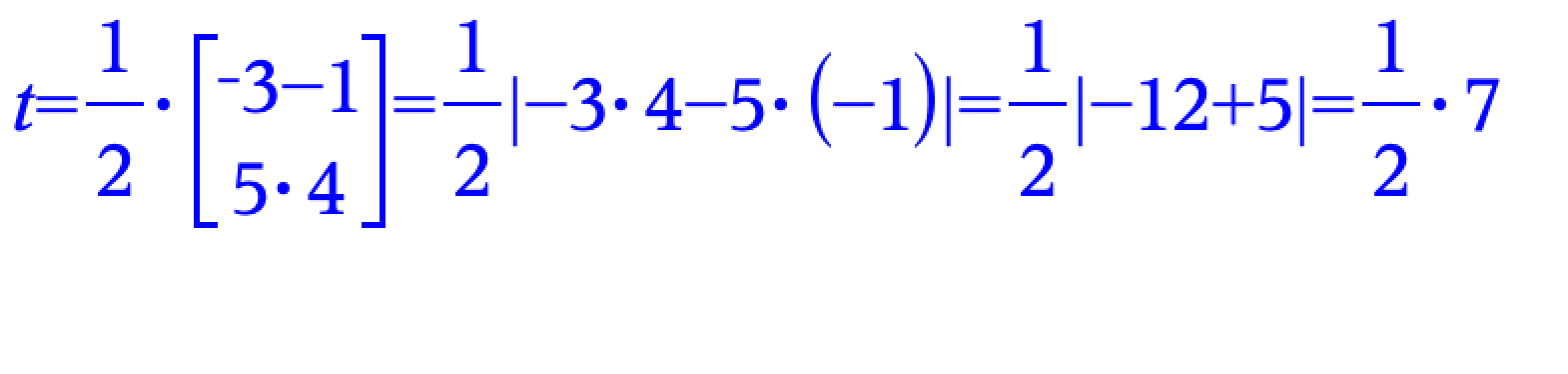
Hvis du skal lave det i Nspire skal du ikke taste egne beregninger, men sætte Nspire til arbejdet.
Desuden er det en vektor, du har skrevet i starten - ikke en determinant.

Start med at sætte oplysningerne ind (med :=)
oa:=[3;0] ob:=[0;5] oc:=[2;t] Semikolon gør, at koordinaterne skrives over hinanden i en 1x2 matix, som i #8, når du trykker Enter. Hvis du adskiller med komma skrives de vandret.

a) Beregn $\overrightarrow{AC}$ : ac:=oc-oa, jf FS side 11 (49)

b) Her skal du bruge en af de andre vektorer i trekanten, fx $\overrightarrow{AB}$ : ab:=ob-oa
Du kan enten gøre som angivet i #10 eller bestemme vinkel A vha. (52) side 11
v_a:=arccos(dotp(ab,ac)/(norm(ab)·norm(ac))|t=4
Derefter kan arealet bestemmes vha. (59) side 12, da trekantens areal er det halve af parallelogrammets areal.
areal:=1/2·abs(norm(ab)·norm(ac)·sin(v_a))|t=4
Denne metode er mere besværlig end den anden, men benytter formler, der bruges i flere andre sammenhænge.

c) Retningsvektor for l r_l:=[2;1]
solve(dotP(r_l,ac=0,t), jf (53) side 11.

Vedhæftet fil:Udklip.JPG

Skriv et svar til: Givet tre punkter

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.