Matematik

Trigonometriske funktioner - harmonisk svingning

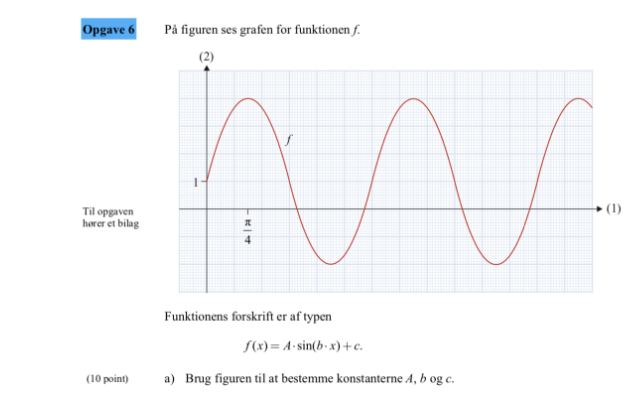
11. februar 2020 af Lei20 (Slettet) - Niveau: A-niveau

Er der nogen, der kan forklare mig, hvad harmonisk svingning går ud på, og hvad de tre konstanter A, b og c i forskriften f(x) = A * sin(b * x) + c fortæller? Hvordan finder man de tre konstanter, hvis grafen for funktionen er givet?

Brugbart svar (0)

Svar #1
11. februar 2020 af MandenMedMangeHatte

Hvad er den største værdi sin(x) kan antage?

Hvad er perioden for sin(x)?

Hvor skærer sin(x) y-aksen?

Brugbart svar (0)

Svar #2
11. februar 2020 af mathon

En harmonisk svingning er karakteriseret ved konstant amplitude $\small A$ og konstant vinkekhastighed/cyklisk frekvens b.

c har betydning for ligevægtsstillingen.

Svar #3
11. februar 2020 af Lei20 (Slettet)

#1 Hvordan kan man se, hvad den største værdi sin(x) kan antage? Hvordan aflæser man perioden?

Den skærer y-aksen i 1.

Brugbart svar (0)

Svar #4
11. februar 2020 af mathon

-1 ≤ sin(x) ≤ 1

$\small b=\frac{2\pi }{T}$

$\small T=\frac{2\pi }{b}$

Svar #5
11. februar 2020 af Lei20 (Slettet)

#4 Kan du prøve at sætte ord på, hvad du gør?

Svar #6
11. februar 2020 af Lei20 (Slettet)

Det drejer sig om denne opgave.

Vedhæftet fil:Skærmbillede 2020-02-11 kl. 18.45.11.png

Brugbart svar (0)

Svar #7
12. februar 2020 af mathon

Brugbart svar (0)

Svar #8
12. februar 2020 af mathon

$\small \begin{array}{llll}&f(x)=3\cdot \sin(2\cdot x)+1 \end{array}$

Brugbart svar (0)

Svar #9
12. februar 2020 af mathon

$\small \begin{array}{llll}\textup{beregning af b:}\\&T=(7.5\, \textup{tern} - 1.5\, \textup{tern})=6\, \textup{tern}\\\\\textup{1.5 tern }=\frac{\pi }{4}\\\textup{hvoraf}\\&T=\frac{\textup{6 tern }}{\textup{1.5 tern }}\cdot \frac{\pi }{4}=4\cdot \frac{\pi }{4}=\pi \\\textup{og}\\&b=\frac{2\pi }{T}=\frac{2\pi }{\pi }=2 \end{array}$

Svar #10
12. februar 2020 af Lei20 (Slettet)

Måden du fandt c på, var det bare ved at se på skæringen med y-aksen? Måden du fandt A var det ved at sige 4-1 ?

Svar #11
12. februar 2020 af Lei20 (Slettet)

Hvad er forskellen på f(x) = A * sin(b * x) + c og f(x) = A * sin(vinkelhastighed * x + faseforskydning) + k? Er de det samme?

Brugbart svar (0)

Svar #12
12. februar 2020 af mathon

at begyndelsesfasen i
$\small f(x)=A\cdot (\sin(b\cdot x)+c\qquad \textup{er 0}$

Brugbart svar (0)

Svar #13
14. februar 2020 af Eksperimentalfysikeren

Den harmoniske svingning kan skrives som f(x) = A * sin(b * x + f) + c

Har man grafen, kan man finde konstanterne på følgende måde:

Aflæs største og mindste værdi. Mindstværdien er -A+c og størsteværdien er A+c. Forskellen er altså 2A, så A er halvdelen af forskellen mellem mindste og største værdi. c er midterværdien mellem mindste og største værdi.

Sinus er periodisk med perioden 2π. Vælg et punkt på kurven og det tilsvarende efter en hel svingning. Find afstanden mellem dem. Denne afstand kaldes T. Det betyder, at f(x+T) = f(x). Det betyder, at b*T = 2π, så b=2π/T.

Find den ikkenegative x-værdi, hvor f er voksende og passerer værdien c. denne værdi er f/b.

Skriv et svar til: Trigonometriske funktioner - harmonisk svingning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.